1 1 2 1 3 1 N
Kalali
Jun 02, 2025 · 2 min read
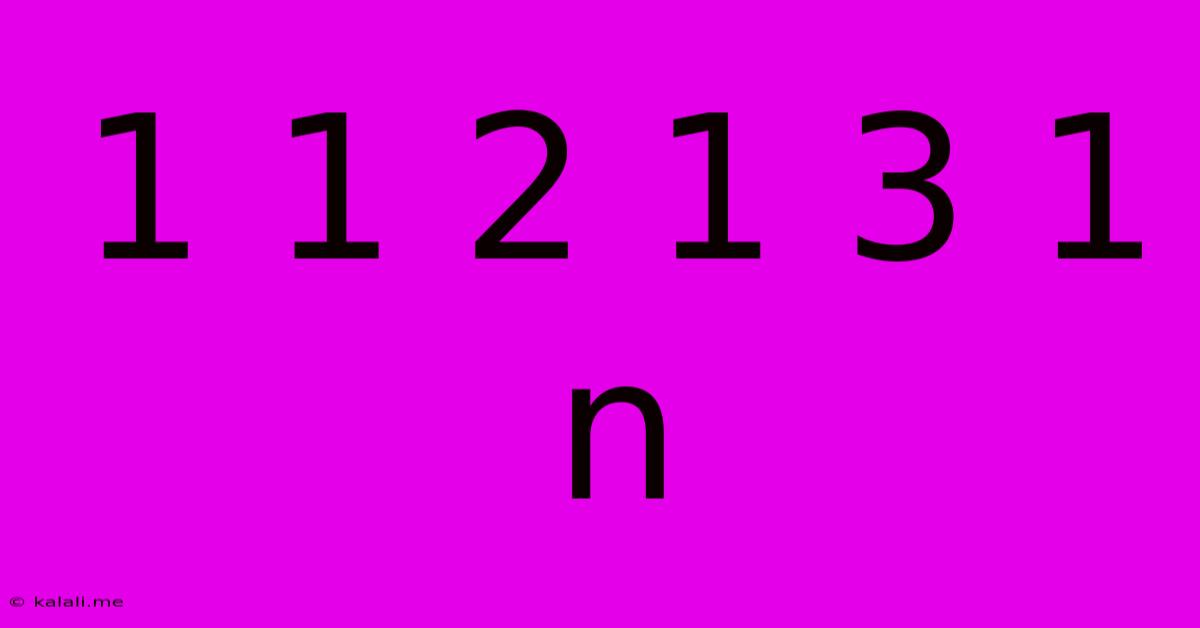
Table of Contents
Decoding the Sequence: Understanding the 1 1 2 1 3 1 n Pattern
This article delves into the fascinating mathematical sequence: 1 1 2 1 3 1 n, exploring its patterns, potential formulas, and its connections to other mathematical concepts. We'll uncover why this seemingly simple sequence holds a surprising amount of mathematical depth and intrigue, perfect for those interested in number theory and pattern recognition.
This sequence, at first glance, might appear random. However, a closer look reveals an underlying structure based on the occurrence of consecutive numbers. Understanding this structure is key to understanding the entire sequence and predicting future terms.
Unveiling the Pattern: Counting Consecutive Numbers
The core of this sequence lies in counting the occurrences of consecutive identical numbers. Let's break down the first few terms:
- 1: There's one '1'.
- 1 1: There are two '1's.
- 2 1 3 1: The '1' appears once again. The next number after '1' is '2', which also appears once. The next consecutive number is 3, which also appears once. And back to '1' again. The sequence becomes 1, 1, 2, 1, 3, 1...
This pattern continues, where each number in the sequence represents the count of consecutive identical numbers that precede it. It's a self-referential sequence, meaning it defines itself through its own terms. This recursive nature makes it both elegant and challenging.
Limitations and Extensions
While the sequence is easily generated for a limited number of terms, predicting the 'n'th term becomes increasingly complex as 'n' grows larger. There isn't a simple, closed-form formula to directly calculate the 'n'th term. Instead, the sequence needs to be generated iteratively, one step at a time.
The concept of extending this sequence infinitely is theoretically possible, but practically challenging due to the rapidly increasing complexity of counting consecutive identical numbers.
Connections to Other Mathematical Concepts
This sequence shares similarities with other self-referential structures in mathematics, such as:
- Look-and-say sequence: While not identical, this sequence shares a similar self-referential nature. The Look-and-say sequence describes the next term by "saying" the previous term (e.g., 1 becomes 11, 11 becomes 21, 21 becomes 1211, and so on).
- Recursive sequences: This sequence is a prime example of a recursive sequence, where each term is defined in terms of previous terms.
Conclusion: A Simple Sequence with Deep Implications
The 1 1 2 1 3 1 n sequence, despite its seemingly simple appearance, exhibits a rich mathematical structure. Its self-referential nature and its iterative generation highlight the elegance and complexity that can be found even within seemingly straightforward numerical patterns. Further exploration of this and similar sequences can open up avenues into more advanced concepts within number theory and recursive algorithms. Understanding this sequence offers a fascinating glimpse into the beauty of mathematical patterns and the power of recursive definitions.
Latest Posts
Latest Posts
-
How Hot Does Car Exhaust Get
Jun 04, 2025
-
Expectation Of A Function Of A Random Variable
Jun 04, 2025
-
Please Provide Abbreviations List As Per Journal
Jun 04, 2025
-
All For One And One For All Synonym
Jun 04, 2025
-
Book Of Jasher Mentioned In The Bible
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 1 3 1 N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.