1 1 2 4 3 9 4
Kalali
Jun 07, 2025 · 2 min read
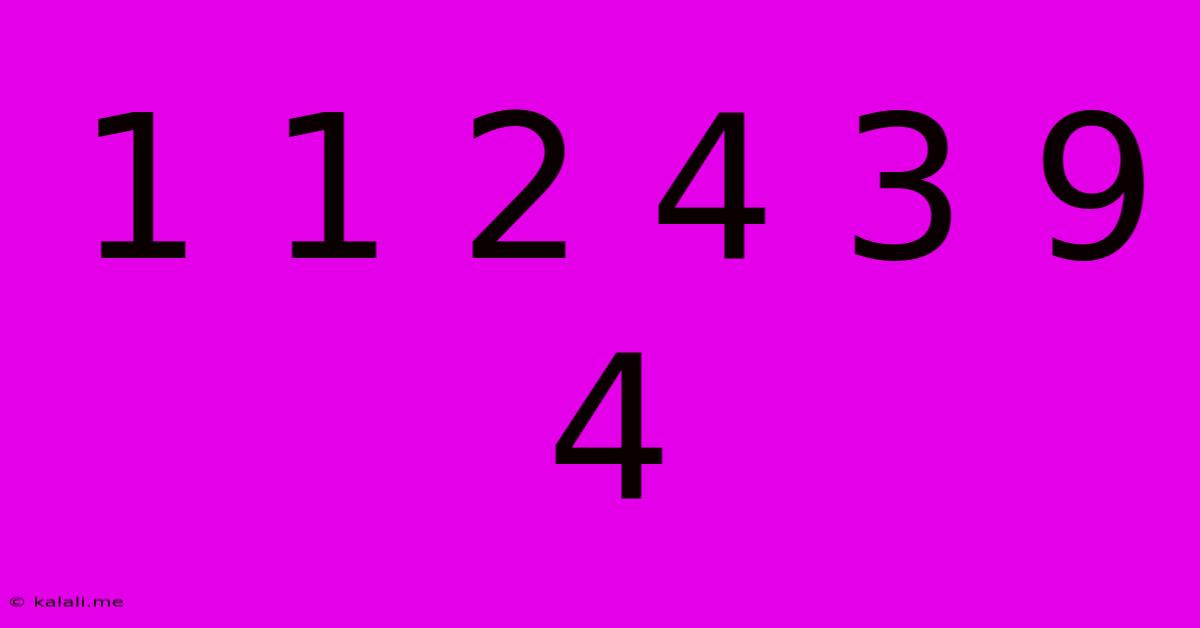
Table of Contents
Unraveling the Pattern: 1 1 2 4 3 9 4 16... and Beyond
This seemingly simple sequence, 1 1 2 4 3 9 4 16..., presents a fascinating puzzle that blends mathematics and pattern recognition. At first glance, it might seem random, but a closer look reveals a clear and elegant underlying principle. This article will explore the pattern, explain its mathematical basis, and delve into its potential extensions and applications. Understanding this sequence can provide insights into fundamental mathematical concepts and problem-solving strategies.
The sequence is based on the concept of squaring. Let's break down the pattern step-by-step:
- 1 1: The sequence begins with the number 1 repeated. This might seem arbitrary, but it establishes the foundation for the pattern.
- 2 4: The next number, 2, is followed by its square, 4 (2 x 2 = 4).
- 3 9: Similarly, 3 is followed by its square, 9 (3 x 3 = 9).
- 4 16: And finally, 4 is followed by its square, 16 (4 x 4 = 16).
Therefore, the complete sequence, extended, is: 1 1 2 4 3 9 4 16 5 25 6 36... and so on.
The Mathematical Rule: A Simple Yet Elegant Solution
The core rule governing this sequence is incredibly straightforward: each odd-numbered term in the sequence is a natural number, and the immediately following even-numbered term is the square of that number.
This simplicity makes the sequence easily understandable and memorable. It's a great example of how seemingly complex patterns can have surprisingly simple explanations. This pattern can also be easily extended indefinitely, showcasing its consistent and predictable nature.
Applications and Extensions: Beyond the Basics
While the sequence might seem purely mathematical, its underlying principle of squaring has numerous applications in various fields. Understanding this fundamental operation is crucial in:
- Algebra: Squaring is a foundational operation in algebraic manipulations and equation solving.
- Geometry: Calculating areas and volumes often involves squaring measurements.
- Physics: Many physical phenomena involve squared relationships, like the relationship between force and acceleration (Newton's second law).
- Computer Science: Squaring operations are frequently used in algorithms and computations.
Furthermore, variations on this sequence can be created by modifying the initial terms or introducing different mathematical operations. This opens up a world of possibilities for exploring mathematical patterns and their properties.
Conclusion: The Power of Pattern Recognition
The simple sequence 1 1 2 4 3 9 4 16... demonstrates the power of pattern recognition and its importance in understanding mathematical concepts. By identifying the underlying principle of squaring, we can not only understand the sequence itself but also appreciate its wider applications and potential extensions. This simple yet profound example highlights how even basic mathematical concepts can lead to complex and fascinating patterns. This is a great example of the beauty and elegance found within mathematics.
Latest Posts
Latest Posts
-
What Blocks Can Endermen Not Pick Up
Jun 07, 2025
-
How Much Api Calls To Bundle At A Time
Jun 07, 2025
-
Can I Pour Concrete Over 2 Days
Jun 07, 2025
-
What Size Nozzle Does The Anycubic Mega Pro Use
Jun 07, 2025
-
How To Fix Cracked Leather Car Seats
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 4 3 9 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.