1 2 4 8 16 32 64 128
Kalali
Aug 21, 2025 · 6 min read
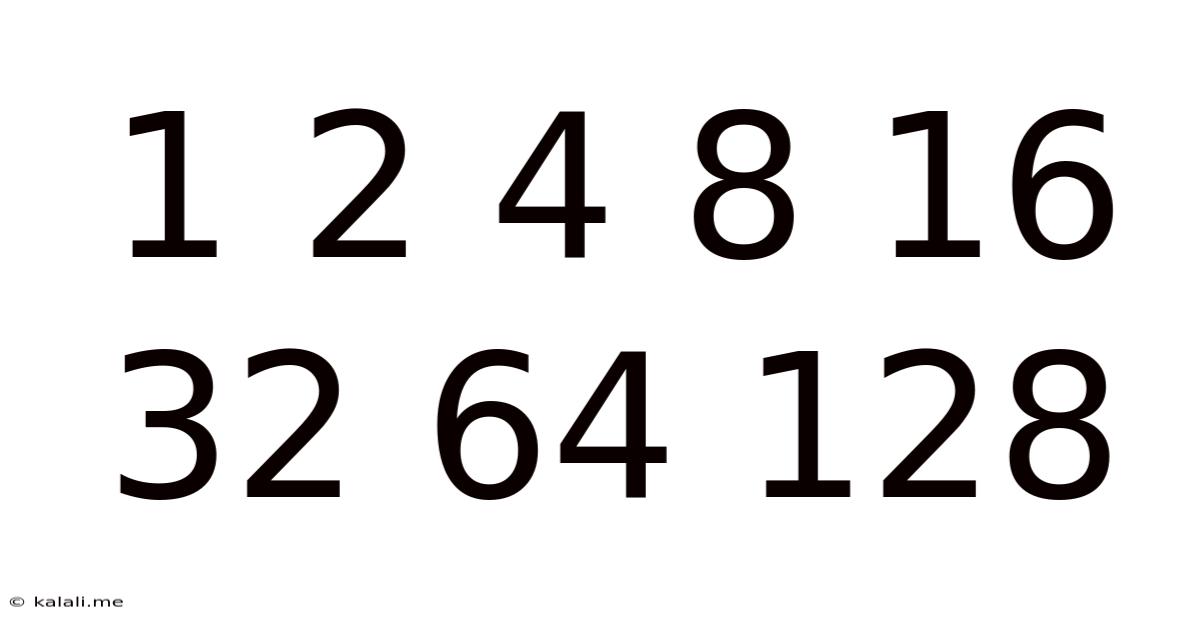
Table of Contents
Decoding the Power of Two: Exploring the Sequence 1, 2, 4, 8, 16, 32, 64, 128... and Beyond
This seemingly simple sequence – 1, 2, 4, 8, 16, 32, 64, 128 – represents far more than just a series of numbers. It's a fundamental building block of mathematics, computer science, and even nature itself. This article delves deep into the significance of this geometric progression, exploring its mathematical properties, its applications in various fields, and its connections to broader concepts in science and technology. We'll uncover why understanding this sequence is crucial for anyone seeking a deeper understanding of the digital world and beyond.
Understanding the Sequence: Exponential Growth
At its core, this sequence is a geometric progression where each term is double the preceding term. Mathematically, it can be represented as 2<sup>n</sup>, where 'n' is the position of the term in the sequence (starting from n=0 for 1). This means we're dealing with exponential growth – a pattern characterized by rapid, multiplicative increases. Unlike arithmetic sequences (like 1, 3, 5, 7…), where the increase is constant, exponential sequences grow increasingly faster. This rapid growth is a key characteristic that underpins many of its applications.
Mathematical Properties and Relationships
The sequence 1, 2, 4, 8, 16, 32, 64, 128, and its continuation, possesses several fascinating mathematical properties:
-
Binary Representation: This is perhaps the most significant property in the digital age. Each number in the sequence directly corresponds to a power of two, forming the basis of the binary number system. Binary is the language of computers, using only 0s and 1s to represent all data. This sequence is fundamental to how computers store and process information. Understanding binary allows us to grasp how digital data, from images to text, is represented and manipulated.
-
Sum of the Sequence: The sum of the first 'n' terms in this sequence is given by the formula 2<sup>n</sup> - 1. For example, the sum of the first four terms (1+2+4+8) is 15, which is 2<sup>4</sup> - 1. This simple formula highlights the elegant mathematical relationships within the sequence.
-
Powers of Two and their Divisibility: Every number in the sequence is a power of two and is perfectly divisible only by other numbers within the sequence (and 1). This characteristic has implications in various fields, from data structures in computer science to the study of prime numbers in mathematics.
-
Relationship to Fibonacci Sequence: While seemingly unrelated at first glance, the sequence of powers of two shares a subtle connection with the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...). Notice how certain Fibonacci numbers appear within the powers of two sequence. This unexpected link highlights the interconnectedness of different mathematical concepts.
Applications in Computer Science and Technology
The sequence 1, 2, 4, 8, 16, 32, 64, 128… and its extension to much larger powers of two, plays a pivotal role in numerous aspects of computer science and technology:
-
Memory and Storage: Computer memory (RAM) and storage devices (hard drives, SSDs) are often organized in powers of two. This is because data is processed and stored in binary format. We commonly see memory sizes like 1GB (Gigabyte), 2GB, 4GB, 8GB, 16GB, and so on. These values directly reflect the efficiency of using powers of two in data management.
-
Data Structures: Many fundamental data structures in computer science, such as binary trees and heaps, are based on the power-of-two principle. The structure and efficiency of these data structures rely on the properties of this sequence.
-
Networking: IP addresses, which identify devices on a network, are often expressed using binary notation, indirectly linked to powers of two. Network protocols and routing algorithms often leverage the structure of powers of two for efficiency and optimization.
-
Algorithms: Numerous algorithms in computer science rely on techniques that involve dividing problems into halves or doubling the size of data structures. These are directly related to the properties of powers of two and contribute to efficient algorithm design. Merge sort, for example, efficiently sorts data by repeatedly splitting it in half.
-
Digital Audio and Video: Digital audio and video encoding and compression techniques often leverage powers of two in their sampling rates, bit depths, and frame sizes. This relates directly to how audio and video data is represented and processed digitally.
Applications Beyond Computers: Science and Nature
The influence of powers of two extends beyond the digital realm; it's surprisingly prevalent in various areas of science and the natural world:
-
Biology: Cellular division in many organisms follows an approximate doubling pattern, reflecting exponential growth. This is seen in the growth of bacterial populations and other rapidly dividing cells.
-
Fractals: Many natural patterns, like branching patterns in trees or the structure of snowflakes, exhibit fractal geometry. Fractals are characterized by self-similarity at different scales, and the principles of doubling and halving are often observed in their structure.
-
Music: Musical scales and intervals often relate to powers of two through the concept of octaves. An octave represents a doubling of frequency, demonstrating a connection to the exponential nature of the sequence.
-
Physics: Certain physical phenomena, like radioactive decay, exhibit exponential decay, the inverse of exponential growth. Understanding exponential growth is therefore crucial to understanding its inverse.
The Sequence Extended: Implications for Large Numbers
While we initially focused on the sequence 1, 2, 4, 8, 16, 32, 64, 128, its implications extend to much larger numbers. As we progress to higher powers of two, we encounter truly enormous numbers that are crucial in various fields:
-
Data storage: Petabytes (PB), exabytes (EB), zettabytes (ZB), and beyond are all units of data storage based on powers of two. The rapid growth of digital data means that understanding these massive scales is essential.
-
Computational complexity: The runtime and memory requirements of algorithms often scale exponentially. Understanding powers of two is crucial for assessing the feasibility of computing tasks involving massive datasets.
-
Cryptography: Modern cryptography relies heavily on large prime numbers and other mathematical concepts that are related to the properties of powers of two and exponential growth. This underlines the significance of this sequence in securing digital communications.
Conclusion: A Fundamental Building Block
The seemingly simple sequence 1, 2, 4, 8, 16, 32, 64, 128… is far from simple. It's a fundamental building block of mathematics, computer science, and various other fields. Its applications range from the basic principles of computing to the complexities of modern cryptography and the patterns observed in the natural world. Understanding this sequence and its properties provides valuable insights into the exponential growth observed in many areas of science and technology. From the smallest bits of digital information to the vast scales of data storage, the power of two continues to shape our world in profound ways. Its significance underscores the beauty and utility of seemingly simple mathematical concepts in addressing complex challenges and unlocking the secrets of the universe, both digital and natural.
Latest Posts
Latest Posts
-
Select The Preferred Method For Placing Orders
Aug 21, 2025
-
Which Idea Is Clearly Associated With The Title Of Endgame
Aug 21, 2025
-
3 Quarter Of A Million Dollars In Numbers
Aug 21, 2025
-
Animal Beginning With N In The Rainforest
Aug 21, 2025
-
United States That Start With A Vowel
Aug 21, 2025
Related Post
Thank you for visiting our website which covers about 1 2 4 8 16 32 64 128 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.