1 2 6 24 120 ...
Kalali
Jun 13, 2025 · 2 min read
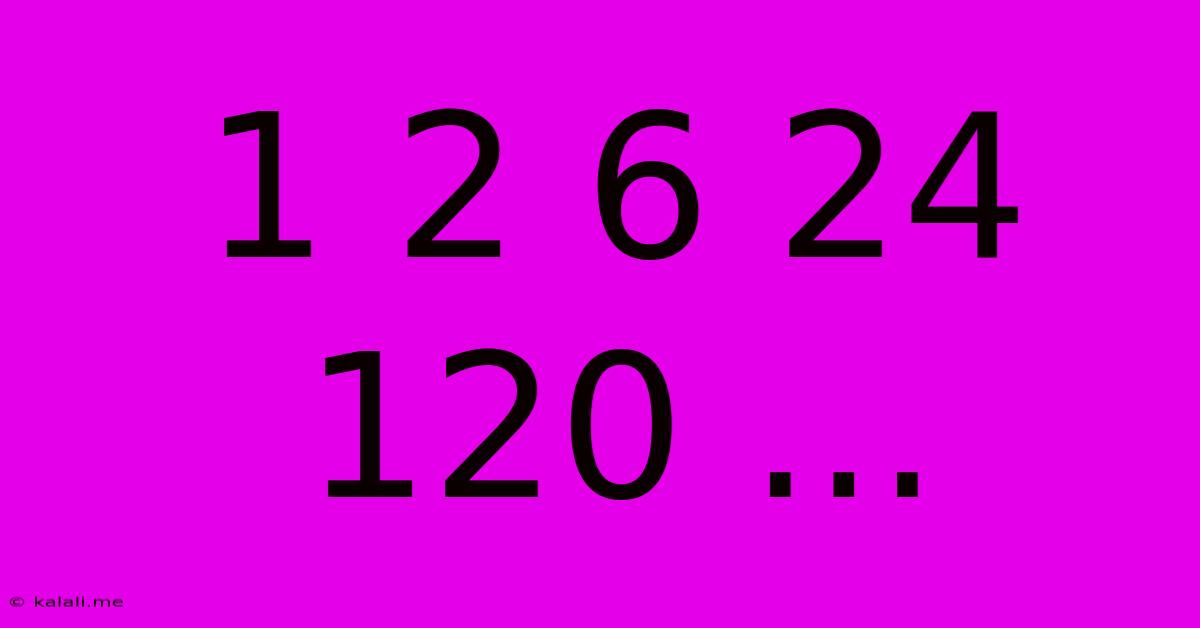
Table of Contents
Decoding the Sequence: 1, 2, 6, 24, 120... and Understanding Factorial Numbers
This article delves into the fascinating mathematical sequence: 1, 2, 6, 24, 120... Understanding this sequence unlocks a fundamental concept in mathematics: factorials. This exploration will cover the definition of factorials, how to calculate them, and their applications in various fields. We'll also look at how to identify and continue this type of sequence.
What are Factorial Numbers?
The sequence 1, 2, 6, 24, 120... represents the factorial sequence. A factorial, denoted by an exclamation mark (!), is the product of all positive integers less than or equal to a given positive integer. For example:
- 1! = 1
- 2! = 2 × 1 = 2
- 3! = 3 × 2 × 1 = 6
- 4! = 4 × 3 × 2 × 1 = 24
- 5! = 5 × 4 × 3 × 2 × 1 = 120
And so on. Essentially, each number in the sequence is the product of itself and all preceding positive integers.
Calculating Factorials
Calculating factorials is straightforward for smaller numbers. However, as the numbers increase, manual calculation becomes tedious. Most calculators and programming languages (like Python, Java, and JavaScript) have built-in functions to calculate factorials efficiently. For instance, in Python, you'd use the math.factorial() function.
Applications of Factorials
Factorials have significant applications across various mathematical and scientific fields, including:
-
Combinatorics and Probability: Factorials are fundamental in calculating permutations and combinations, crucial in probability and statistics. For example, determining the number of ways to arrange n distinct objects.
-
Calculus: Factorials appear in Taylor and Maclaurin series expansions of functions, essential tools in calculus.
-
Statistics: Factorials are used in various statistical distributions, including the Poisson distribution and the binomial distribution.
-
Science and Engineering: They appear in numerous scientific formulas, particularly in fields like quantum mechanics and chemical kinetics.
Identifying and Continuing the Sequence
To identify if a sequence follows the factorial pattern, look for the characteristic multiplicative relationship between consecutive terms. Each term is obtained by multiplying the previous term by the next integer.
For example, to continue the sequence beyond 120, we would calculate 6!:
- 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
The next number in the sequence would be 720, followed by 5040 (7!), and so on.
In Conclusion
Understanding factorial numbers is essential for anyone working with mathematics, statistics, or computer science. Their applications are widespread and fundamental to many important calculations and concepts. By recognizing the pattern and understanding the definition, you can easily identify and continue this unique and valuable mathematical sequence.
Latest Posts
Latest Posts
-
40 Percent Of What Number Is 60
Jun 14, 2025
-
What Is The Chemical Name For Chalk
Jun 14, 2025
-
Which Of The Following Is Not Part Of The Brain
Jun 14, 2025
-
What Can 51 Be Divided By
Jun 14, 2025
-
What Occupies Space And Has Mass
Jun 14, 2025
Related Post
Thank you for visiting our website which covers about 1 2 6 24 120 ... . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.