1/2 Divided By 3 In Fraction Form
Kalali
Jul 23, 2025 · 5 min read
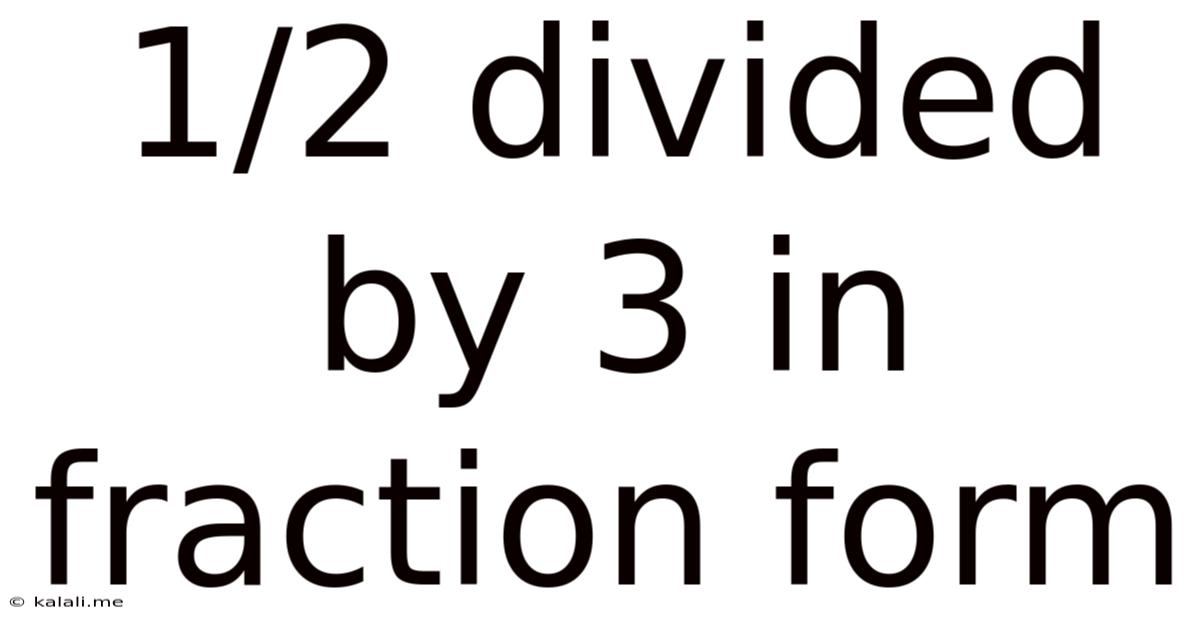
Table of Contents
1/2 Divided by 3: A Comprehensive Guide to Fraction Division
Understanding fraction division is a cornerstone of mathematical literacy. While it might seem daunting at first, mastering this concept unlocks a world of problem-solving possibilities. This article provides a comprehensive explanation of how to solve 1/2 divided by 3, exploring various approaches and offering insights into the underlying principles of fraction division. We'll delve into the mechanics, explore real-world applications, and address common misconceptions, ensuring you gain a firm grasp of this fundamental arithmetic operation.
What does 1/2 divided by 3 even mean?
Before jumping into the calculation, let's clarify what the problem represents. The expression "1/2 divided by 3" asks: "If we divide one-half into three equal parts, what is the size of each part?" This translates to finding a fraction representing a third of one-half. This is a crucial understanding, providing a visual context that simplifies the abstract nature of fraction division. Think of splitting a pizza slice (1/2) into three equal pieces – what fraction of the whole pizza does each piece represent?
Method 1: Using the "Keep, Change, Flip" Method (Reciprocal)
This popular method simplifies fraction division by transforming it into multiplication. The process involves three steps:
- Keep: Keep the first fraction (dividend) as it is: 1/2
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (divisor) – find its reciprocal. The reciprocal of 3 (or 3/1) is 1/3.
Therefore, the problem becomes: 1/2 × 1/3
Now, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 1) / (2 × 3) = 1/6
Therefore, 1/2 divided by 3 equals 1/6.
Method 2: Visual Representation – Dividing the Fraction
Visual aids can significantly enhance understanding. Imagine a rectangle representing one whole. Shade half of it to represent 1/2. Now, divide this shaded half into three equal parts. Each part will represent 1/6 of the original whole rectangle. This visual demonstration reinforces the numerical result obtained using the "Keep, Change, Flip" method.
Method 3: Understanding Division as Repeated Subtraction
Division can also be viewed as repeated subtraction. How many times can you subtract 3 from 1/2? This approach isn't as straightforward with fractions, but it helps illustrate the concept. We can't directly subtract 3 from 1/2 because 3 is larger. However, we can think of dividing 1/2 into thirds, which leads us back to the "Keep, Change, Flip" method and the same solution of 1/6.
Why the "Keep, Change, Flip" Method Works
The "Keep, Change, Flip" method isn't just a trick; it's grounded in mathematical principles. Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by swapping its numerator and denominator. This method efficiently converts the division of fractions into a multiplication problem, making it easier to calculate.
Applications of Fraction Division in Real Life
Fraction division isn't just an abstract mathematical exercise; it's vital for solving practical problems in everyday life. Here are a few examples:
-
Cooking and Baking: Recipes often require dividing ingredients. If a recipe calls for 1/2 cup of flour and you want to make only 1/3 of the recipe, you'd need to calculate (1/2) ÷ 3 = 1/6 cup of flour.
-
Sewing and Crafting: Cutting fabric or other materials often involves fractional measurements. Dividing a piece of fabric into equal sections requires understanding fraction division.
-
Construction and Engineering: Many projects involve precise measurements and calculations with fractions. Dividing materials or spaces into fractional parts is essential for accuracy.
-
Data Analysis and Statistics: Working with datasets often involves calculating averages and proportions, which often require operations with fractions.
Common Mistakes to Avoid
While the "Keep, Change, Flip" method is relatively straightforward, some common errors can occur:
-
Forgetting to flip the second fraction: This is the most frequent error. Remember that you're multiplying by the reciprocal, not the original fraction.
-
Incorrect multiplication of fractions: Make sure to multiply numerators with numerators and denominators with denominators. Avoid multiplying numerators with denominators or vice-versa.
-
Simplifying fractions improperly: Always simplify the resulting fraction to its lowest terms.
Extending the Concept: Dividing Fractions by Other Fractions
The principles discussed above extend to dividing any fraction by another fraction. For example, let's consider the problem 2/3 divided by 1/4. Following the "Keep, Change, Flip" method:
- Keep: 2/3
- Change: ×
- Flip: 4/1
The problem becomes: (2/3) × (4/1) = 8/3 or 2 2/3
This same methodology can be applied to any division problem involving fractions, solidifying your understanding of this fundamental mathematical concept.
Conclusion
Mastering fraction division is a crucial skill with far-reaching applications. By understanding the underlying principles and employing the efficient "Keep, Change, Flip" method, you can confidently tackle a wide range of problems involving fractions. Remember the visual representations and avoid common mistakes to solidify your understanding. With practice and consistent application, you'll become proficient in this essential area of mathematics. The ability to effortlessly manipulate fractions opens doors to more complex mathematical concepts and real-world problem-solving. So, keep practicing, and you'll soon find that fraction division becomes second nature. Remember to always simplify your answers to their lowest terms for the most accurate and concise representation.
Latest Posts
Latest Posts
-
How Much Did A House Cost In 1920
Jul 24, 2025
-
What Is 2 To The Seventh Power
Jul 24, 2025
-
How Many Pallets Can Fit In A 53 Foot Trailer
Jul 24, 2025
-
How Long Does Mayo Last After Expiration Date
Jul 24, 2025
-
What Size Is 14 16 In Juniors In Womens
Jul 24, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.