1 3 2 3 N 3
Kalali
May 24, 2025 · 3 min read
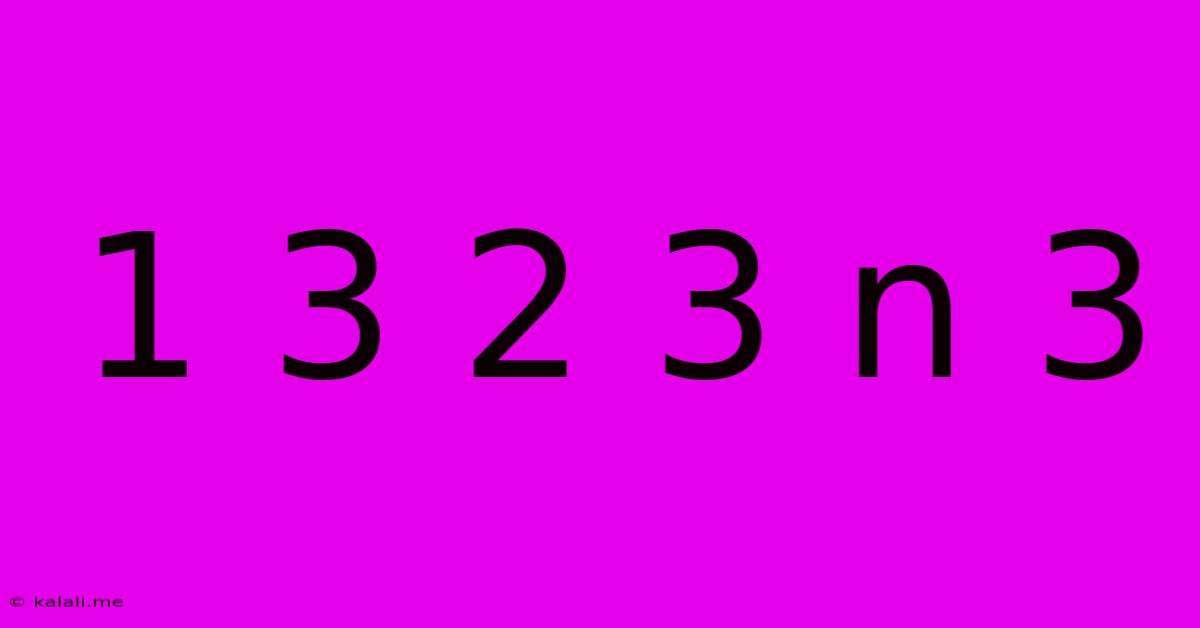
Table of Contents
Decoding the Sequence: 1 3 2 3 n 3 – Unveiling the Pattern and its Applications
This article delves into the intriguing numerical sequence: 1, 3, 2, 3, n, 3. We'll explore potential patterns, analyze possible solutions for 'n', and discuss the broader implications of such sequences in mathematics and computer science. Understanding sequences like this is crucial for various fields, from algorithm optimization to cryptography.
What Makes This Sequence Unique?
At first glance, the sequence 1, 3, 2, 3, n, 3 appears arbitrary. However, the key to unlocking its mystery lies in identifying underlying patterns or rules governing its progression. Unlike simple arithmetic or geometric progressions, this sequence requires a more nuanced approach. We need to consider potential relationships between consecutive numbers, differences between them, or even the possibility of a recursive definition.
Possible Interpretations and Solutions for 'n'
Several interpretations could explain this sequence. Let's explore a few possibilities:
-
Alternating Sequences: We could view the sequence as a combination of two interwoven sequences: {1, 2, n} and {3, 3, 3}. If this is the case, 'n' could represent the next logical number in the first subsequence. Without further information, however, this approach offers limited certainty.
-
Modular Arithmetic: Perhaps the sequence is based on modulo operations. Analyzing the remainders after division by a certain number could reveal a pattern. However, testing various moduli doesn't immediately lead to a conclusive solution.
-
Recursive Relationships: A recursive approach defines each term based on previous terms. While finding a simple recursive relationship is challenging, more complex recursive formulas involving multiple previous terms might explain the sequence. This approach would require a deeper mathematical analysis.
-
Context is Key: The most likely scenario is that this sequence is incomplete or lacks essential context. The value of 'n' might depend on the source or problem where this sequence originates. It could be part of a larger, more complex series, or it might represent a specific coded message.
Applications in Different Fields:
Understanding numerical sequences is crucial in several fields:
-
Computer Science: Sequences are fundamental in algorithm design and analysis. Efficient algorithms often rely on recognizing and exploiting patterns in data sequences.
-
Mathematics: Number theory extensively studies sequences to explore properties of numbers and their relationships.
-
Cryptography: Sequences play a significant role in cryptography, where complex sequences are used for encryption and decryption. Analyzing unknown sequences is essential for code-breaking and security analysis.
-
Data Analysis: Identifying patterns in data sequences is a core aspect of data analysis and machine learning. Algorithms analyze sequences to predict future trends or extract valuable insights.
Conclusion: The Need for Further Information
The sequence 1, 3, 2, 3, n, 3 presents an intriguing puzzle. Without further information or context, definitively determining the value of 'n' remains elusive. However, by exploring various mathematical concepts and analyzing potential patterns, we've gained a better understanding of the methods used to decipher such sequences. The exercise highlights the importance of considering multiple perspectives and the crucial role of context in solving mathematical problems. The value of 'n' ultimately depends on the application or context within which this sequence appears. More information is needed to reach a definitive conclusion.
Latest Posts
Latest Posts
-
What Is The Easter Bunny Favorite Color
Jun 30, 2025
-
How Much Is 100 Gallons Of Diesel
Jun 30, 2025
-
How Much Is 50 Gallons Of Water
Jun 30, 2025
-
How Many Laps Around A Football Field Is A Mile
Jun 30, 2025
-
The Ability To Say Clever And Funny Things
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about 1 3 2 3 N 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.