1 3 4 7 11 18 29
Kalali
Jul 06, 2025 · 5 min read
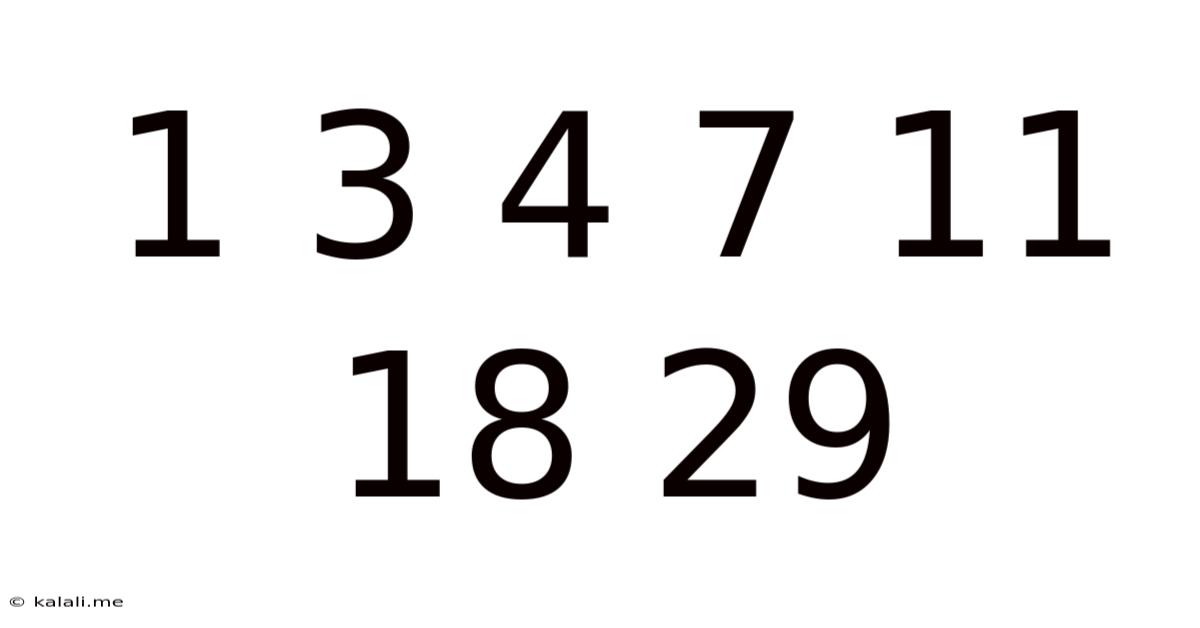
Table of Contents
Unraveling the Mystery: The Sequence 1, 3, 4, 7, 11, 18, 29... and the Power of Recursive Patterns
This seemingly simple sequence of numbers – 1, 3, 4, 7, 11, 18, 29 – hides a fascinating mathematical pattern that's both elegant and powerful. Understanding this pattern unlocks not only the secrets behind this specific sequence but also reveals broader concepts within mathematics, particularly recursive relationships and their applications in various fields. This article will delve deep into the sequence, exploring its underlying structure, predicting future numbers, and examining its connections to other mathematical concepts. We will also touch upon how understanding such patterns can improve analytical and problem-solving skills.
What is the pattern?
At first glance, the sequence might appear random. However, a closer inspection reveals a recursive relationship: each number (after the first two) is the sum of the two preceding numbers. This is a key characteristic of the Fibonacci sequence, a famous mathematical series with widespread applications in nature, art, and computer science. While not identical to the Fibonacci sequence (which starts 1, 1, 2...), this sequence shares its fundamental recursive nature.
- 1 + 3 = 4
- 3 + 4 = 7
- 4 + 7 = 11
- 7 + 11 = 18
- 11 + 18 = 29
This recursive definition allows us to effortlessly extend the sequence indefinitely. Simply add the last two numbers to generate the next one. This simple yet powerful rule is the heart of this numerical puzzle.
Predicting Future Numbers in the Sequence
Armed with the recursive rule, predicting future numbers becomes a straightforward process. Let's calculate the next few numbers in the sequence:
- 29 + 18 = 47
- 47 + 29 = 76
- 76 + 47 = 123
- 123 + 76 = 199
- 199 + 123 = 322
And so on. The possibilities are endless, showcasing the generative power of recursive relationships. This predictability is a hallmark of structured mathematical sequences, allowing for accurate forecasting and analysis.
Beyond Simple Addition: Exploring Deeper Connections
While the recursive rule provides a simple way to generate the sequence, understanding its deeper connections to other mathematical concepts enriches our comprehension. For instance, the sequence can be expressed using a recurrence relation:
- a<sub>n</sub> = a<sub>n-1</sub> + a<sub>n-2</sub> (where a<sub>0</sub> = 1 and a<sub>1</sub> = 3)
This formula provides a concise mathematical representation of the sequence's generation process. Recurrence relations are powerful tools used extensively in various fields, including computer science (for algorithm design), physics (for modeling dynamic systems), and economics (for predicting economic trends).
Applications and Real-World Examples of Recursive Patterns
Recursive patterns aren't just abstract mathematical curiosities; they're fundamental to understanding and modeling numerous real-world phenomena. Consider these examples:
-
Branching Structures in Nature: The branching patterns of trees, rivers, and even blood vessels often exhibit recursive characteristics. Each branch or tributary can be seen as a smaller version of the main structure, repeating the pattern on a smaller scale.
-
Fractals: Fractals are geometric shapes that exhibit self-similarity at different scales. The classic Mandelbrot set is a prime example of a fractal generated through a recursive process. The intricate detail and complexity arise from the repeated application of a simple recursive rule.
-
Computer Algorithms: Many computer algorithms rely on recursion to solve problems efficiently. Examples include searching algorithms, sorting algorithms, and graph traversal algorithms. Recursion's power lies in its ability to break down complex problems into smaller, self-similar subproblems.
-
Financial Modeling: Recursive models are used extensively in financial modeling to predict future stock prices, interest rates, and other financial variables. These models incorporate various factors and use recursive relationships to project future outcomes.
-
Population Growth: Simple population growth models often utilize recursive relationships to project population size over time, considering factors such as birth rates, death rates, and migration.
Developing Analytical and Problem-Solving Skills through Sequence Analysis
Analyzing sequences like 1, 3, 4, 7, 11, 18, 29 enhances critical thinking and problem-solving abilities. The process of identifying patterns, formulating hypotheses, and testing those hypotheses is crucial for developing strong analytical skills. Here's how this sequence analysis contributes:
-
Pattern Recognition: Identifying the recursive relationship requires keen observation and attention to detail. This skill is transferable to many other areas, including data analysis, code debugging, and scientific research.
-
Logical Reasoning: Formulating the recurrence relation involves logical deduction and the ability to express patterns concisely using mathematical notation.
-
Predictive Modeling: The ability to predict future numbers in the sequence builds the foundation for predictive modeling in various domains. This skill is invaluable in forecasting, planning, and decision-making.
-
Abstract Thinking: Understanding the underlying structure of the sequence encourages abstract thinking, the ability to grasp concepts independently of concrete examples.
Further Exploration and Extensions
This sequence, though seemingly simple, opens doors to exploring more complex mathematical concepts. For instance:
-
Generating Functions: Generating functions are powerful tools used to represent sequences mathematically. They provide a compact way to encode the entire sequence and can be used to derive various properties.
-
Matrix Representation: The sequence can also be represented using matrices, offering an alternative way to compute future terms and analyze the sequence's properties.
-
Convergence and Limits: While this sequence grows unboundedly, understanding the concept of convergence and limits in similar recursive sequences is a key aspect of advanced mathematical analysis.
Conclusion:
The sequence 1, 3, 4, 7, 11, 18, 29, while seemingly simple at first, unveils a fascinating world of recursive patterns and their far-reaching implications. Understanding its recursive nature not only allows us to predict future numbers but also provides insights into broader mathematical concepts with applications across various disciplines. Furthermore, the process of analyzing such sequences significantly sharpens analytical and problem-solving skills, crucial tools for navigating complexities in any field. This exploration underscores the power of observation, logical reasoning, and the beauty of mathematical patterns hidden in plain sight. The ability to uncover and understand these patterns is a key skill for anyone seeking to improve their analytical prowess and problem-solving capabilities. The seemingly simple sequence acts as a gateway to a much larger world of mathematical exploration and practical application.
Latest Posts
Latest Posts
-
What Do You Call An Old Snowman
Jul 06, 2025
-
K H D U D C M
Jul 06, 2025
-
How Many Jalapeno Peppers In A Pound
Jul 06, 2025
-
The Definition Of A Circle Uses The Undefined Term
Jul 06, 2025
-
Four Letter Word With Q At The End
Jul 06, 2025
Related Post
Thank you for visiting our website which covers about 1 3 4 7 11 18 29 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.