1/3 To The Power Of 3
Kalali
Apr 06, 2025 · 5 min read
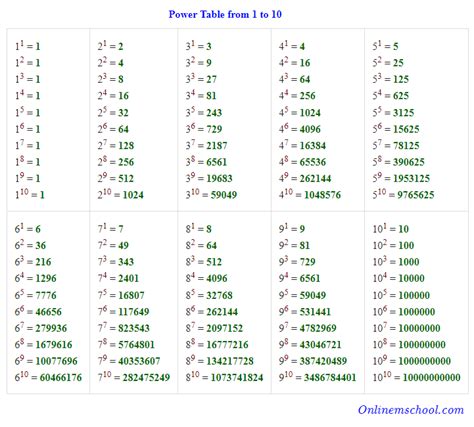
Table of Contents
1/3 to the Power of 3: A Deep Dive into Exponents and Fractions
Understanding exponents and fractions is fundamental to grasping many mathematical concepts. This article delves into the seemingly simple calculation of (1/3)³, exploring its meaning, the methods for solving it, and its broader implications within the realm of mathematics and beyond. We'll uncover the intricacies of this calculation and examine its relevance in various applications.
What Does (1/3)³ Actually Mean?
Before we delve into the calculation itself, let's clarify what (1/3)³ signifies. The expression represents the cube of the fraction 1/3. In simpler terms, it means multiplying the fraction 1/3 by itself three times: (1/3) × (1/3) × (1/3). This concept extends to any number raised to a power (exponent); the exponent indicates how many times the base number is multiplied by itself.
Understanding Exponents
Exponents, also known as powers or indices, are a concise way of representing repeated multiplication. The general form is bⁿ, where 'b' is the base and 'n' is the exponent. The exponent dictates how many times the base is multiplied by itself. For instance:
- 2³ = 2 × 2 × 2 = 8
- 5² = 5 × 5 = 25
- (1/2)² = (1/2) × (1/2) = 1/4
The exponent '3' in (1/3)³ signifies that we are cubing the fraction 1/3. Understanding this fundamental concept is key to solving the problem.
Calculating (1/3)³: Step-by-Step Guide
Now, let's systematically calculate (1/3)³. There are two primary methods:
Method 1: Direct Multiplication of Fractions
This method involves multiplying the numerator (top number) and the denominator (bottom number) separately.
- Multiply the numerators: 1 × 1 × 1 = 1
- Multiply the denominators: 3 × 3 × 3 = 27
- Combine the results: The result is 1/27.
Therefore, (1/3)³ = 1/27.
Method 2: Applying the Power to Numerator and Denominator Separately
This method leverages the property that (a/b)ⁿ = aⁿ/bⁿ. We can apply the exponent to both the numerator and the denominator individually.
- Apply the exponent to the numerator: 1³ = 1
- Apply the exponent to the denominator: 3³ = 27
- Combine the results: This yields 1/27.
This method demonstrates the fundamental rule of exponents when dealing with fractions, providing an alternative approach to reach the same solution.
Visualizing (1/3)³: A Geometric Approach
The concept of (1/3)³ can also be visualized geometrically. Imagine a cube with sides of length 1 unit. Now, imagine dividing each side of this cube into three equal parts. This creates a smaller cube within the larger one. The volume of this smaller cube represents (1/3)³. Since the side length of the smaller cube is 1/3, its volume is (1/3) × (1/3) × (1/3) = 1/27 of the volume of the original cube. This visual representation reinforces the numerical result we obtained earlier.
Expanding on the Concept: Negative Exponents and Fractional Exponents
Our exploration of (1/3)³ can be expanded to include more complex scenarios involving negative and fractional exponents.
Negative Exponents
A negative exponent signifies the reciprocal of the base raised to the positive exponent. For example, (1/3)⁻³ = 1/(1/3)³ = 27. This highlights the inverse relationship between positive and negative exponents.
Fractional Exponents
Fractional exponents introduce the concept of roots. For example, (1/3)^(1/2) represents the square root of 1/3. Understanding fractional exponents requires a grasp of root operations and their relationship to exponents.
Applications of (1/3)³ and Related Concepts
The seemingly simple calculation of (1/3)³ and related concepts have significant applications across various fields:
- Geometry and Volume Calculations: As demonstrated earlier, this concept is crucial for calculating volumes of cubes and other three-dimensional shapes.
- Probability and Statistics: Fractions and exponents frequently appear in probability calculations, representing the likelihood of specific events.
- Physics and Engineering: Exponents are essential in many physics formulas, such as those describing motion, electricity, and magnetism.
- Finance and Economics: Compound interest calculations heavily rely on exponential functions.
- Computer Science: Exponential growth and decay models are crucial in analyzing algorithm efficiency and data structures.
Beyond the Calculation: Mastering Exponents and Fractions
The calculation of (1/3)³ is more than just a simple arithmetic exercise. It serves as a gateway to understanding broader mathematical concepts. Mastering exponents and fractions is crucial for success in higher-level mathematics and related disciplines. A firm grasp of these concepts will unlock more complex mathematical ideas and pave the way for a deeper understanding of the world around us.
Practical Tips for Mastering Exponents and Fractions
- Practice regularly: Consistent practice is key to internalizing these concepts. Work through various examples and problems.
- Visualize: Utilize visual aids, such as geometric representations, to solidify your understanding.
- Break down complex problems: Divide complex problems into smaller, manageable steps.
- Seek help when needed: Don't hesitate to seek assistance from teachers, tutors, or online resources.
- Connect concepts: Establish connections between exponents, fractions, and other mathematical topics.
Conclusion: The Significance of a Simple Calculation
(1/3)³ may seem like a trivial calculation, but its implications are far-reaching. Understanding this seemingly simple problem unlocks a deeper appreciation for exponents, fractions, and their applications in various fields. By mastering these fundamental concepts, you lay a strong foundation for future mathematical endeavors and develop crucial skills applicable in many areas of life. The journey from a simple calculation to a broader understanding is a testament to the power of mathematical exploration and the importance of building a solid foundation in fundamental principles. So, embrace the challenge, explore the nuances, and unlock the world of mathematics!
Latest Posts
Latest Posts
-
How Long Is 70 Cm In Inches
Apr 06, 2025
-
Blood Type A And O Punnett Square
Apr 06, 2025
-
How Many Pints In 1 2 Gallon
Apr 06, 2025
-
1 Galon Is How Many Millileters
Apr 06, 2025
-
What Percentage Of 80 Is 60
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about 1/3 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.