1 4 9 16 25 36
Kalali
May 10, 2025 · 2 min read
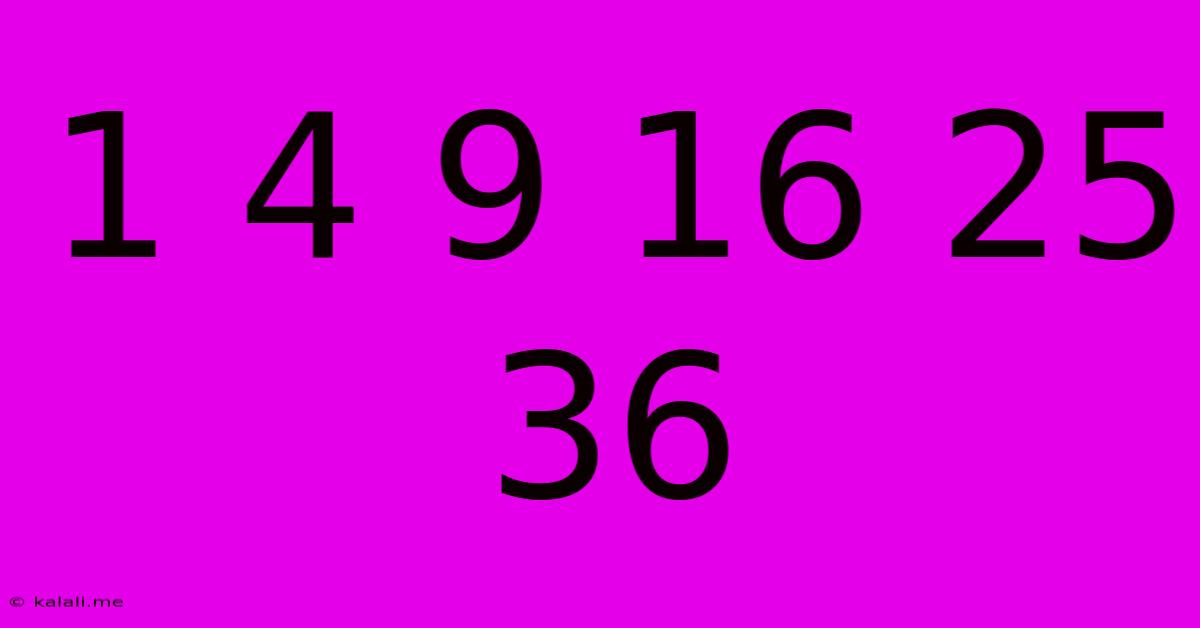
Table of Contents
Decoding the Sequence: 1 4 9 16 25 36
This seemingly simple sequence, 1 4 9 16 25 36, holds a significant mathematical concept that's both fascinating and foundational. This article will explore this sequence, uncovering its pattern, its mathematical underpinnings, and its applications. Understanding this sequence is a stepping stone to grasping more complex mathematical ideas.
What is the Pattern?
The sequence 1 4 9 16 25 36 represents the sequence of perfect squares. Each number is the square of a consecutive integer:
- 1 = 1²
- 4 = 2²
- 9 = 3²
- 16 = 4²
- 25 = 5²
- 36 = 6²
This means each number is the result of multiplying an integer by itself. This fundamental mathematical operation forms the basis of many other mathematical concepts.
Mathematical Significance of Perfect Squares
Perfect squares are crucial in various mathematical fields:
- Geometry: They are directly related to area calculations. For instance, a square with a side length of 3 units has an area of 9 square units (3²).
- Algebra: Perfect squares are essential in simplifying algebraic expressions, particularly when factoring quadratic equations. Recognizing perfect square trinomials allows for quicker and easier solutions.
- Number Theory: Perfect squares play a vital role in number theory, influencing concepts like Pythagorean triples and Diophantine equations.
- Calculus: Understanding squares is foundational for understanding higher-level mathematical concepts like derivatives and integrals.
Extending the Sequence and Finding the nth Term
The sequence can be extended indefinitely. The next few terms would be 49 (7²), 64 (8²), 81 (9²), and so on.
To find the nth term in this sequence, we simply use the formula: n². For example, the 10th term would be 10² = 100. This formula allows for easy calculation of any term within the sequence.
Applications in Real-World Scenarios
While seemingly abstract, perfect squares find applications in various real-world scenarios:
- Construction and Engineering: Calculating areas, volumes, and dimensions often involve perfect squares.
- Computer Science: In algorithms and data structures, the concept of squaring is used frequently.
- Physics: Many physics formulas, especially those related to motion and energy, incorporate squared values.
Conclusion:
The seemingly simple sequence 1 4 9 16 25 36, representing perfect squares, is a cornerstone of mathematics with far-reaching implications. Understanding its pattern and significance opens doors to comprehending more complex mathematical ideas and their applications across various fields. This fundamental sequence serves as a building block for more advanced mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
How Much Is 10 Miles In Minutes
Jul 18, 2025
-
How Much Is 48 Oz Of Water
Jul 18, 2025
-
How Long Does It Take To Drive 2000 Miles
Jul 18, 2025
-
How Many Grams In A Teaspoon Of Cinnamon
Jul 18, 2025
-
How Long To Heat Water In Microwave
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about 1 4 9 16 25 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.