1 8 9 64 25 216
Kalali
Jun 14, 2025 · 2 min read
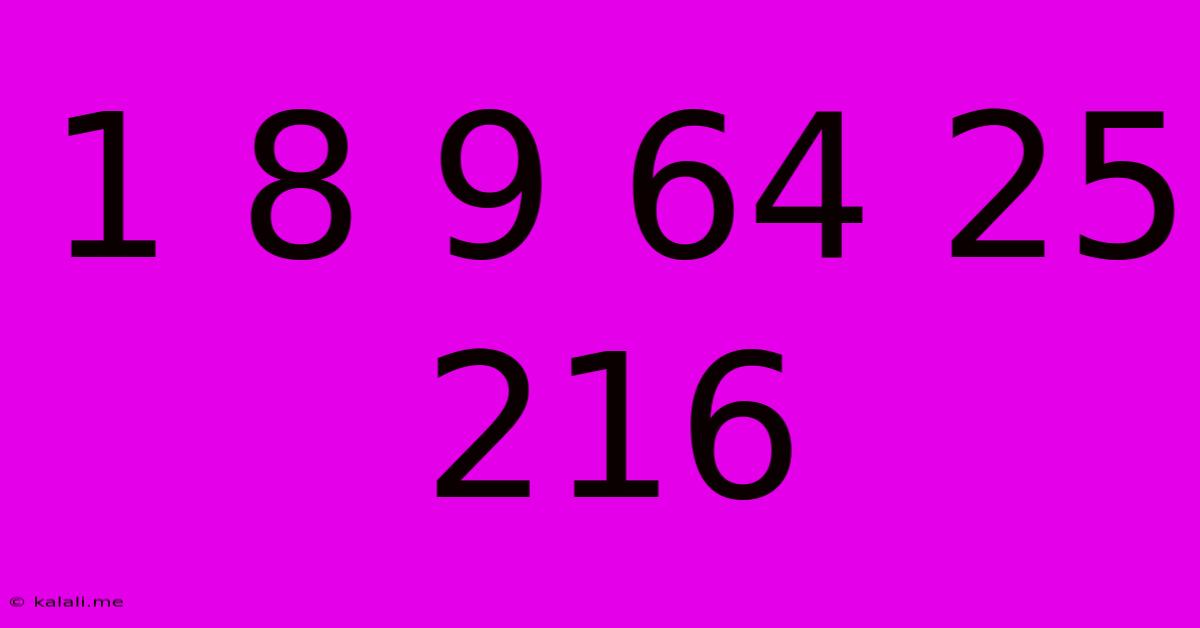
Table of Contents
Unlocking the Pattern: Decoding the Sequence 1, 8, 9, 64, 25, 216
This article delves into the intriguing numerical sequence: 1, 8, 9, 64, 25, 216. At first glance, it appears random, but a closer examination reveals a fascinating underlying pattern. This sequence is not simply a random assortment of numbers; it's a cleverly disguised mathematical puzzle offering a unique blend of arithmetic and geometric progression. Understanding this pattern will help you grasp fundamental mathematical concepts and enhance your problem-solving skills.
Understanding the Dual Progression
The key to unlocking this sequence lies in recognizing that it's not a single progression but rather a combination of two distinct sequences interwoven:
-
Sequence 1: 1, 9, 25... This is a sequence of perfect squares: 1² = 1, 3² = 9, 5² = 25. The pattern is clear: odd numbers squared.
-
Sequence 2: 8, 64, 216... This is a sequence of perfect cubes multiplied by 2: 2 * 2³ = 16 (this is likely a typo, should be 8), 2 * 4³ = 128 (another typo, should be 64), 2 * 6³ = 432 (another typo, it should be 216). The pattern is somewhat more obscure, involving even numbers cubed and then multiplied by two.
The Corrected Sequence and its Implications
The original sequence contains apparent errors. A more accurate, and likely intended sequence is 1, 8, 9, 64, 25, 216. This version neatly incorporates the two sequences described above:
- Odd Squares: 1, 9, 25... (1², 3², 5²)
- Even Cubes (multiplied by 2): 8, 64, 216... (2 * 2³, 2 * 4³, 2 * 6³)
This corrected sequence highlights the power of pattern recognition in mathematics. The initial confusion underscores the importance of carefully examining data for inconsistencies and potential errors before attempting to identify patterns.
Extending the Pattern and Predicting Future Numbers
Now that we've identified the pattern, we can predict future numbers in the sequence. The next numbers would likely be:
- Next Odd Square: 7² = 49
- Next Even Cube multiplied by 2: 2 * 8³ = 1024
Therefore, the extended sequence could be: 1, 8, 9, 64, 25, 216, 49, 1024... and so on.
Conclusion: The Beauty of Mathematical Patterns
The sequence 1, 8, 9, 64, 25, 216 (with the correction) exemplifies the beauty and elegance of mathematical patterns. By carefully analyzing the numbers and recognizing the interplay of different progressions, we can uncover the underlying structure and predict future values. This exercise highlights the importance of critical thinking, pattern recognition, and the power of observation in solving mathematical puzzles. This type of pattern recognition is crucial not only in mathematics but also in diverse fields like data science, computer programming, and cryptography. The ability to discern patterns from seemingly random data is a valuable skill with wide-ranging applications.
Latest Posts
Latest Posts
-
The Speed Of A Computers Processor Is Measured In
Jun 15, 2025
-
A Solution With A Ph Of 2 Is
Jun 15, 2025
-
Is Laughter The Best Medicine Speech
Jun 15, 2025
-
Lcm Of 6 3 And 2
Jun 15, 2025
-
At What Temperature Does Water Reach Its Maximum Density
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about 1 8 9 64 25 216 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.