1 And 1 2 Divided By 2
Kalali
Jul 02, 2025 · 5 min read
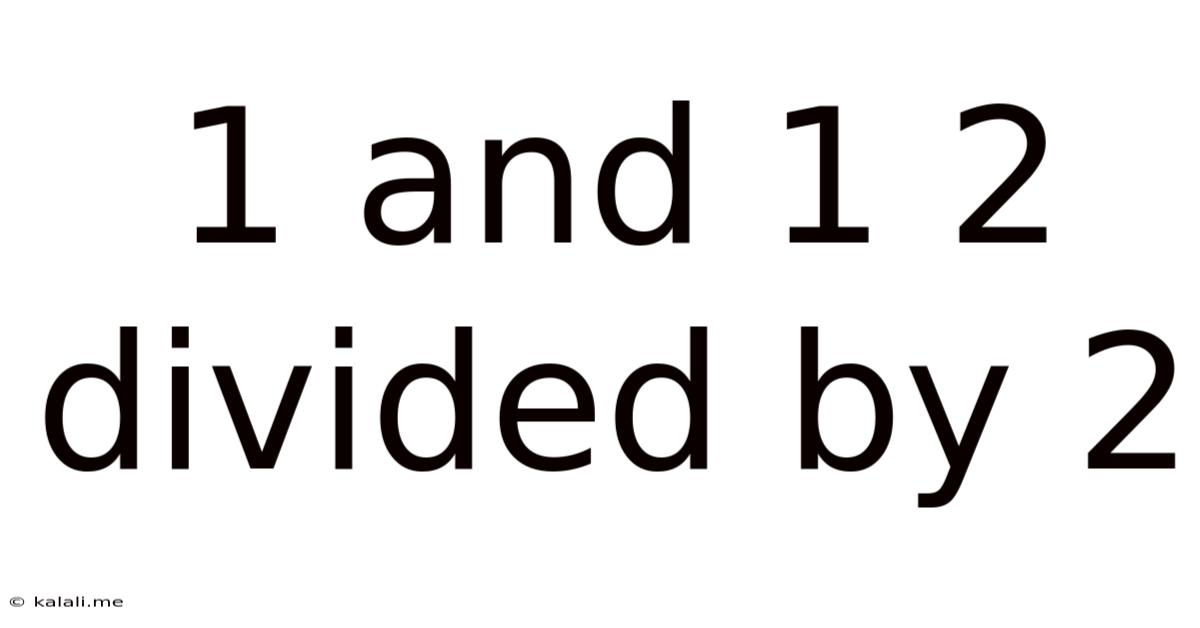
Table of Contents
Decoding the Seemingly Simple: A Deep Dive into 1 and 1/2 Divided by 2
This seemingly simple mathematical problem, "1 and 1/2 divided by 2," can actually be a gateway to understanding several crucial mathematical concepts. While the answer itself is straightforward, the various approaches to solving it illuminate different aspects of fractions, decimals, and division. This article will explore multiple methods of solving this problem, discuss the underlying principles, and highlight the importance of understanding these foundational mathematical concepts. We'll also look at how this type of problem can be applied to real-world scenarios.
Meta Description: Learn multiple ways to solve the seemingly simple math problem "1 and 1/2 divided by 2," understanding fractions, decimals, and division along the way. This comprehensive guide explores different approaches and real-world applications.
Understanding the Problem: Fractions and Division
Before diving into the solutions, let's first clarify the problem. We are asked to divide one and a half (1 ½) by two (2). This involves understanding how to work with fractions and how division operates with them. The core challenge lies in efficiently handling the mixed number (1 ½) – a combination of a whole number and a fraction.
Method 1: Converting to Improper Fraction
This is a common and efficient method for solving division problems involving mixed numbers. The first step is to convert the mixed number (1 ½) into an improper fraction.
-
Step 1: Convert to Improper Fraction: To convert 1 ½ to an improper fraction, we multiply the whole number (1) by the denominator (2) and add the numerator (1). This gives us 3. We then place this result over the original denominator, resulting in the improper fraction 3/2.
-
Step 2: Perform the Division: Now we have a straightforward fraction division problem: (3/2) ÷ 2. Remember that dividing by a number is the same as multiplying by its reciprocal. The reciprocal of 2 is ½. Therefore, the problem becomes (3/2) x (1/2).
-
Step 3: Multiply the Fractions: Multiply the numerators together (3 x 1 = 3) and the denominators together (2 x 2 = 4). This gives us the fraction 3/4.
Therefore, 1 ½ divided by 2 equals 3/4.
Method 2: Converting to Decimals
Another approach involves converting both the mixed number and the divisor into decimals. This method can be particularly helpful when working with a calculator or when dealing with more complex fractions.
-
Step 1: Convert to Decimals: Convert 1 ½ to its decimal equivalent, which is 1.5.
-
Step 2: Perform the Division: Now we perform the decimal division: 1.5 ÷ 2.
-
Step 3: Calculate the Result: Using a calculator or long division, we find that 1.5 divided by 2 equals 0.75.
This decimal, 0.75, is equivalent to the fraction 3/4, confirming our previous result.
Method 3: Visual Representation with Models
A visual approach can be particularly helpful for understanding the concept, especially for those who are new to fractions. Imagine a pizza cut into four slices. 1 ½ represents three of these slices. Dividing these three slices among two people means each person gets 3/4 of a pizza, visually reinforcing the solution. This method is excellent for solidifying understanding, particularly for younger learners.
Method 4: Breaking Down the Problem
This approach involves separating the problem into smaller, more manageable parts. We can divide the whole number (1) by 2 and the fraction (½) by 2 separately, then adding the results.
-
Step 1: Divide the Whole Number: 1 divided by 2 equals ½.
-
Step 2: Divide the Fraction: ½ divided by 2 is equivalent to ½ multiplied by ½, which equals ¼.
-
Step 3: Combine the Results: Adding the results from Step 1 and Step 2, we have ½ + ¼ = ¾.
This approach demonstrates a different way of tackling the problem and showcases the distributive property of division.
Real-World Applications
The seemingly simple calculation of 1 ½ divided by 2 has numerous practical applications:
-
Baking and Cooking: Recipes frequently require dividing ingredients. If a recipe calls for 1 ½ cups of flour and you want to halve the recipe, you'll need to calculate 1 ½ cups divided by 2, resulting in ¾ cups of flour.
-
Sharing Resources: Imagine you have 1 ½ pizzas and want to share them equally among two people. Each person receives ¾ of a pizza.
-
Measurement and Construction: In construction or other areas involving measurements, you might need to divide lengths or quantities. For example, if a piece of wood is 1 ½ meters long and needs to be divided into two equal parts, each part will be ¾ meters long.
-
Finance and Budgeting: Allocating budgets or resources often involves dividing amounts. For instance, if you have $1.50 and want to split it evenly between two people, each receives $0.75.
-
Data Analysis and Statistics: Averaging data or calculating proportions frequently involves division. This concept is crucial in various fields, including scientific research, market analysis, and engineering.
Expanding the Understanding: Further Exploration
Understanding this basic problem opens the door to more complex scenarios. Consider similar problems with different numbers:
-
2 ½ divided by 3: This problem would require similar steps, involving conversion to improper fractions or decimals before performing the division.
-
3 ¾ divided by 5: This further extends the complexity, demanding a strong understanding of fraction manipulation and division.
Exploring these variations strengthens the foundational mathematical skills needed for more advanced calculations.
Conclusion: Mastering the Fundamentals
The problem of 1 ½ divided by 2, while seemingly basic, provides a valuable opportunity to practice and reinforce fundamental mathematical concepts. By exploring different methods of solution – from converting to improper fractions and decimals to using visual models and breaking down the problem – we deepen our understanding of fractions, decimals, and division. This understanding extends far beyond the classroom, proving essential in numerous real-world applications. Mastering these fundamental concepts builds a strong mathematical foundation, enabling greater confidence and competence in tackling more challenging problems in the future. Remember, the key to mastering mathematics is practice and a thorough understanding of the underlying principles.
Latest Posts
Latest Posts
-
How Many Laps Is 300 Yards In A Pool
Jul 30, 2025
-
Only Letter Not In A State Name
Jul 30, 2025
-
How Many Weeks Are In 9 Years
Jul 30, 2025
-
How Many Pennies Fit In A 5 Gallon Water Jug
Jul 30, 2025
-
How Many Pounds In 2 Cubic Feet Of Mulch
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about 1 And 1 2 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.