1 In 6 As A Percentage
Kalali
Apr 10, 2025 · 5 min read
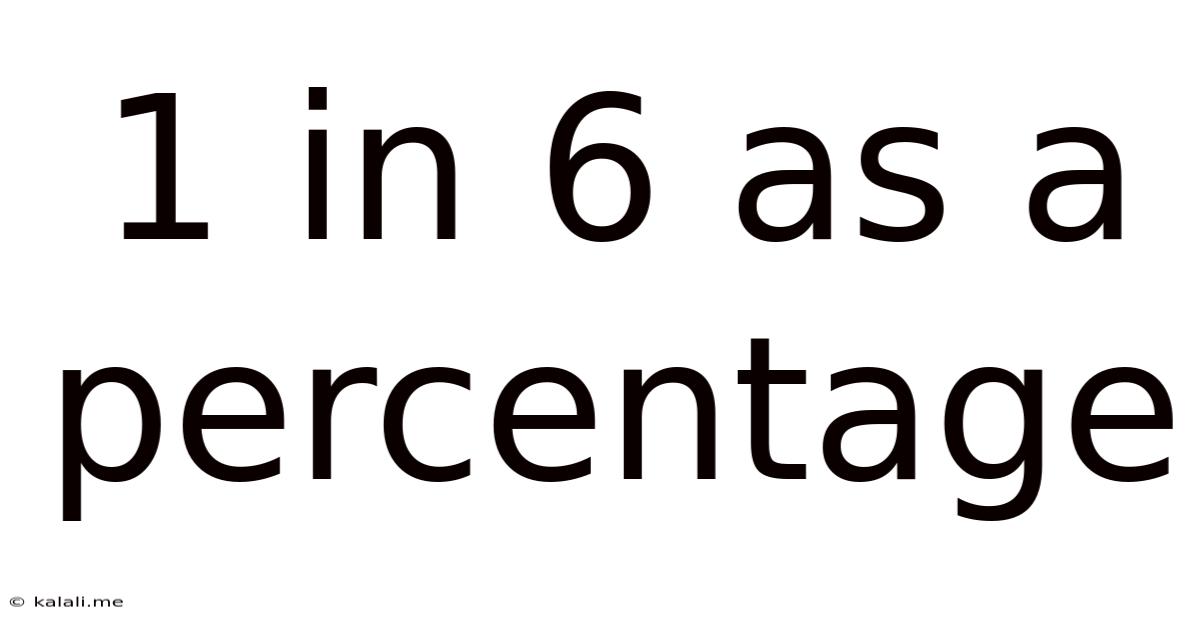
Table of Contents
Decoding 1 in 6: Understanding Fractions, Percentages, and Their Real-World Applications
Understanding fractions and their percentage equivalents is a fundamental skill with far-reaching applications in various aspects of life. This article delves deep into the conversion of the fraction 1 in 6 to a percentage, exploring the mathematical process, practical examples, and the broader implications of such conversions in everyday situations and specialized fields. We'll also explore related concepts like ratios and proportions to provide a comprehensive understanding of this common numerical representation.
What does "1 in 6" actually mean?
Before jumping into the percentage calculation, let's clarify the meaning of the phrase "1 in 6." This expression represents a ratio or a fraction. It signifies that out of a total of six possibilities or events, one specific event is expected to occur. For instance, if you have a six-sided die, the probability of rolling a specific number (let's say, a 3) is 1 in 6. This means there's one favorable outcome (rolling a 3) out of six possible outcomes (rolling a 1, 2, 3, 4, 5, or 6).
Converting 1 in 6 to a percentage:
To convert the fraction 1 in 6 (which can be written as 1/6) into a percentage, we need to follow these steps:
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (6). 1 ÷ 6 = 0.166666... (the 6 repeats infinitely).
-
Multiply the decimal by 100: This step converts the decimal to a percentage. 0.166666... × 100 = 16.6666...%
-
Round the percentage (if necessary): Depending on the level of precision required, you can round the percentage. Rounding to two decimal places, we get 16.67%.
Therefore, 1 in 6 is equivalent to approximately 16.67%.
Understanding the Significance of 16.67%:
This percentage represents a relatively low probability or proportion. It indicates that the event described by "1 in 6" is less likely to occur than events represented by higher percentages. Understanding this significance is crucial in various contexts:
-
Risk Assessment: In fields like healthcare, finance, and engineering, accurately assessing risk is vital. If a certain procedure or investment has a failure rate of 1 in 6, understanding the 16.67% probability helps in making informed decisions and implementing risk mitigation strategies.
-
Data Analysis: In statistical analysis, interpreting percentages is fundamental. A survey showing that 1 in 6 people prefer a particular product translates to a 16.67% market share. This information allows businesses to understand consumer preferences and adjust their marketing strategies accordingly.
-
Probability and Gambling: Games of chance often involve probabilities expressed as fractions. Understanding the percentage equivalent helps in calculating expected returns and assessing the fairness of a game. For instance, in a lottery with a 1 in 6 chance of winning, the probability of winning is only 16.67%.
-
Quality Control: In manufacturing, a 1 in 6 defect rate represents a 16.67% failure rate. This information is crucial for identifying and addressing quality control issues within the production process.
Real-World Applications of 1 in 6 and Percentage Conversions:
Let's explore some real-world scenarios where understanding "1 in 6" and its percentage equivalent (approximately 16.67%) is critical:
-
Medical Studies: A clinical trial might reveal that 1 in 6 patients experienced a specific side effect from a new medication. This 16.67% incidence rate is essential for informing patients about potential risks and for assessing the drug's overall safety profile.
-
Environmental Studies: If a study indicates that 1 in 6 bird species in a particular region are endangered, the 16.67% figure highlights the severity of the conservation challenge and the need for immediate action.
-
Public Health Initiatives: Public health campaigns often rely on understanding population statistics. If 1 in 6 individuals in a community are unvaccinated against a certain disease, the 16.67% figure informs public health strategies and resource allocation.
-
Social Sciences: Sociological studies might reveal that 1 in 6 individuals in a particular demographic group experience a specific form of social injustice. This 16.67% data point informs policy discussions and interventions aimed at addressing societal inequalities.
-
Financial Markets: Understanding percentages is crucial in investment analysis. If a particular stock has a 1 in 6 chance of underperforming the market, the investor can weigh that 16.67% risk against potential returns.
Beyond 1 in 6: Extending the Concept
The principles discussed for converting 1 in 6 to a percentage are applicable to other fractions as well. Understanding the relationship between fractions, decimals, and percentages allows for flexible conversion and interpretation across various numerical representations. Consider these examples:
-
1 in 10: This converts to 1/10 = 0.10 = 10%
-
1 in 20: This converts to 1/20 = 0.05 = 5%
-
2 in 5: This converts to 2/5 = 0.40 = 40%
-
3 in 4: This converts to 3/4 = 0.75 = 75%
These conversions highlight the importance of being able to fluidly move between different numerical formats to accurately represent and interpret data.
Ratios and Proportions: Expanding the Mathematical Context
The concept of "1 in 6" is fundamentally a ratio. A ratio compares two or more quantities. The ratio 1:6 indicates that there is one part of one thing for every six parts of another. This concept expands into proportions, which are statements of equality between two ratios.
For example, the proportion 1/6 = x/100 can be used to solve for x, which represents the percentage equivalent of 1/6. Solving this proportion leads to x = 100/6 ≈ 16.67%, confirming our earlier calculation. Understanding ratios and proportions provides a more robust mathematical framework for handling such numerical relationships.
Conclusion:
The seemingly simple conversion of "1 in 6" to 16.67% unlocks a wealth of understanding across diverse fields. From assessing risks and analyzing data to making informed decisions in various contexts, mastering this conversion is an essential skill for effective communication and problem-solving. Furthermore, understanding the broader mathematical concepts of ratios and proportions provides a solid foundation for handling similar numerical representations and interpreting their significance in the real world. The ability to effortlessly translate between fractions, decimals, and percentages empowers individuals and professionals to navigate numerical information with confidence and precision.
Latest Posts
Latest Posts
-
Cuanto Es 5 6 Pies En Metros
Apr 18, 2025
-
How Many Inches Are In 180 Cm
Apr 18, 2025
-
What Is 11 25 As A Percent
Apr 18, 2025
-
How Much Feet Is 172 Cm
Apr 18, 2025
-
How Many Inches Is 5 8 Cm
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 1 In 6 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.