1 Is What Percent Of 12
Kalali
Apr 22, 2025 · 5 min read
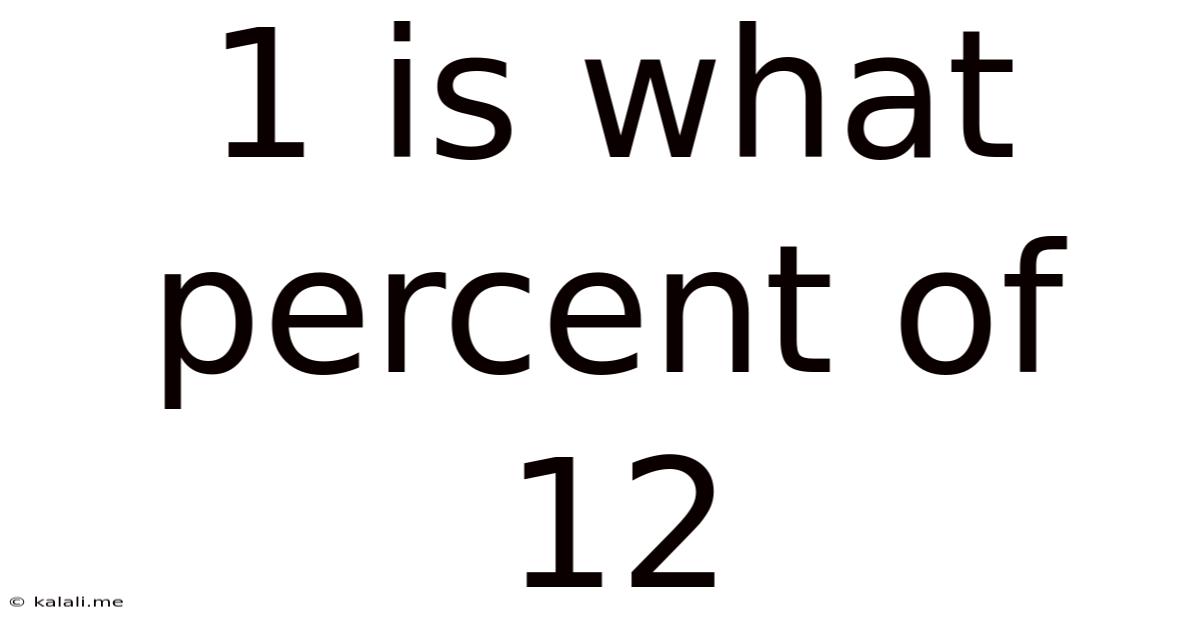
Table of Contents
1 is What Percent of 12? A Deep Dive into Percentages and Their Applications
This seemingly simple question – "1 is what percent of 12?" – opens the door to a fascinating exploration of percentages, their mathematical underpinnings, and their ubiquitous applications in various fields. Understanding how to calculate percentages is a fundamental skill with far-reaching implications in everyday life, from calculating discounts and taxes to understanding financial reports and analyzing statistical data. This article will not only answer the initial question but also delve into the broader context of percentages, exploring their calculation, real-world examples, and common pitfalls to avoid.
Meta Description: Learn how to calculate percentages and understand the significance of this fundamental mathematical concept. This comprehensive guide answers the question "1 is what percent of 12?" and explores various real-world applications.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be represented as a decimal or a fraction. For example, 50% is equivalent to 0.5 or 1/2.
This understanding forms the basis for solving percentage problems. We often encounter scenarios where we need to determine what percentage one number represents of another. This usually involves three key elements:
- The part: The number that represents a fraction of the whole. In our initial question, "1" is the part.
- The whole: The total amount or the base number. In our question, "12" is the whole.
- The percentage: The fraction expressed as a percentage of the whole. This is what we need to calculate.
Calculating "1 is What Percent of 12?"
To determine what percentage 1 represents of 12, we follow these steps:
-
Formulate the equation: We can express the problem as a fraction: 1/12.
-
Convert the fraction to a decimal: Divide the part (1) by the whole (12): 1 ÷ 12 ≈ 0.0833
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.0833 × 100 ≈ 8.33%
Therefore, 1 is approximately 8.33% of 12.
Different Approaches to Percentage Calculations
While the method above is straightforward, there are other ways to approach percentage calculations, each with its own advantages depending on the context:
-
Using Proportions: We can set up a proportion:
x/100 = 1/12. Solving for x gives us the percentage. Cross-multiplying, we get12x = 100, and solving for x yieldsx ≈ 8.33. -
Using the Percentage Formula: The formula is often written as:
(Part / Whole) * 100 = Percentage. Substituting our values, we have:(1/12) * 100 ≈ 8.33%.
Choosing the most suitable method depends on personal preference and the complexity of the problem. For simple calculations like "1 is what percent of 12?", the direct division method is often the quickest and easiest.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous everyday situations:
-
Financial Matters: Calculating discounts, sales tax, interest rates, tips, and returns on investments all involve percentage calculations. Understanding percentage changes (increases or decreases) is crucial for analyzing financial statements and making informed decisions. For instance, calculating the interest earned on a savings account or understanding the APR (Annual Percentage Rate) on a loan relies heavily on percentage computations.
-
Retail and Sales: Discount percentages are frequently used to attract customers. Determining the final price after a discount requires understanding how to calculate percentages. Salespeople also need to calculate commissions, often based on a percentage of their sales.
-
Statistics and Data Analysis: Percentages are fundamental in representing and interpreting data. They allow for easy comparison of proportions within different datasets. For example, expressing survey results as percentages makes it easier to understand the distribution of opinions or preferences. Analyzing market share, evaluating survey results, or understanding growth rates all involve percentages.
-
Science and Engineering: Percentages are used extensively in various scientific and engineering calculations. For instance, determining the concentration of a solution, measuring efficiency, or expressing error margins often utilizes percentages. In chemistry, expressing the concentration of a solution as a percentage is common.
-
Everyday Life: Calculating the percentage of tasks completed, estimating the portion of a budget spent on specific items, or understanding nutritional information on food labels all involve percentage calculations.
Common Pitfalls and Mistakes to Avoid
While percentage calculations are relatively simple, several common mistakes can lead to inaccurate results:
-
Confusing the Part and the Whole: Ensuring you correctly identify the "part" and the "whole" is crucial. Mistaking one for the other will lead to an incorrect answer.
-
Incorrect Decimal-to-Percentage Conversion: Remember to multiply the decimal by 100 to convert it to a percentage. Forgetting this step is a common error.
-
Rounding Errors: When rounding off decimals, be mindful of potential inaccuracies. Rounding too early in the calculation can lead to significant deviations in the final answer.
-
Using Incorrect Formulas: Using the wrong formula or applying the formula incorrectly can produce erroneous results.
Advanced Percentage Applications: Percentage Change and Percentage Point Change
Beyond simple percentage calculations, understanding percentage change and percentage point change is crucial for interpreting data effectively.
-
Percentage Change: This measures the relative change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100. This indicates the percentage increase or decrease between two points in time. It's commonly used in financial reporting and economic analysis. -
Percentage Point Change: This represents the absolute difference between two percentages. For instance, if the interest rate increases from 5% to 8%, the percentage point change is 3 (8% - 5% = 3%). While seemingly simple, it’s crucial to distinguish this from a percentage change, which would calculate the relative increase.
Understanding the distinction between these two concepts is critical for accurately interpreting data and avoiding misinterpretations.
Conclusion: Mastering Percentages for a Data-Driven World
The seemingly simple question, "1 is what percent of 12?", serves as a gateway to understanding the broader significance of percentage calculations. From everyday financial decisions to complex scientific analyses, the ability to calculate and interpret percentages is a vital skill. By understanding the underlying principles, mastering different calculation methods, and being aware of common pitfalls, you can confidently navigate the numerous situations where percentages play a crucial role. The ability to accurately calculate and interpret percentages empowers individuals to make informed decisions in various aspects of life, both personal and professional, in our increasingly data-driven world. So, next time you encounter a percentage problem, remember the fundamentals and approach it with confidence.
Latest Posts
Latest Posts
-
1 Cup Of Sour Cream Is How Many Ounces
Apr 23, 2025
-
15 Is What Percent Of 18
Apr 23, 2025
-
28 C Is What In Fahrenheit
Apr 23, 2025
-
How Many Atoms Are In H2
Apr 23, 2025
-
Cuantos Pies Tiene Un Acre De Terreno
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.