10 Is What Percent Of 30
Kalali
Apr 26, 2025 · 5 min read
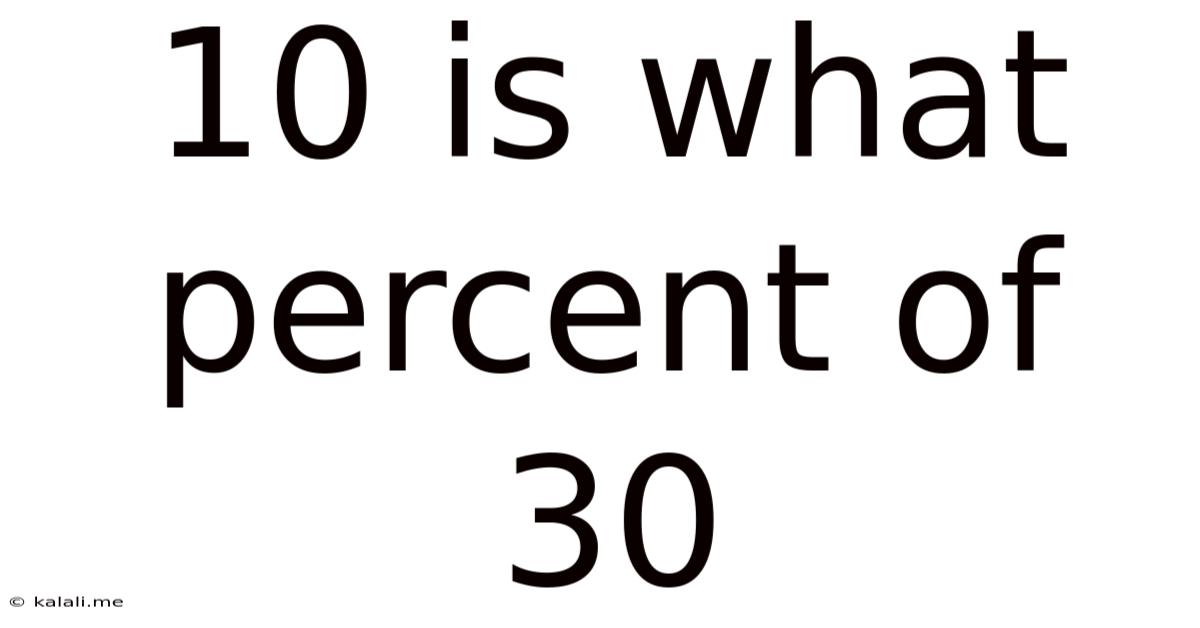
Table of Contents
10 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life, from understanding discounts and sales to analyzing financial data and interpreting statistics. This article will delve into the seemingly simple question, "10 is what percent of 30?", providing a detailed explanation of the calculation process, exploring different methods, and offering real-world examples to solidify your understanding. We'll also look at related percentage problems and discuss how to confidently tackle similar challenges. By the end, you'll not only know the answer but also possess a robust understanding of percentage calculations.
What this article will cover:
- Understanding the fundamentals of percentages
- Step-by-step calculation: 10 is what percent of 30?
- Alternative methods for calculating percentages
- Practical applications of percentage calculations
- Advanced percentage problems and solutions
- Troubleshooting common mistakes in percentage calculations
- Resources for further learning
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Percentages are a convenient way to represent proportions and are widely used to express changes, rates, and proportions in various contexts. For example, a 10% discount means you save 10 out of every 100 units of currency. Understanding this basic concept is crucial for solving percentage problems.
Step-by-Step Calculation: 10 is What Percent of 30?
To determine what percent 10 is of 30, we need to follow these steps:
-
Set up the equation: We can express the problem as a fraction: 10/30. This represents the part (10) over the whole (30).
-
Convert the fraction to a decimal: Divide the part (10) by the whole (30): 10 ÷ 30 = 0.3333... (this is a repeating decimal).
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.3333... × 100 = 33.33...%
-
Round (if necessary): For practical purposes, we often round percentages. Rounding to two decimal places, we get 33.33%. Therefore, 10 is approximately 33.33% of 30.
Therefore, the answer to the question "10 is what percent of 30?" is approximately 33.33%.
Alternative Methods for Calculating Percentages
While the above method is straightforward, there are other approaches to solve percentage problems. Let's explore a couple of alternatives:
-
Using Proportions: You can set up a proportion to solve for the unknown percentage (x):
10/30 = x/100
Cross-multiply: 30x = 1000
Solve for x: x = 1000/30 = 33.33...%
-
Using the Percentage Formula: The basic percentage formula is:
(Part / Whole) * 100 = Percentage
Substituting the values from our problem:
(10 / 30) * 100 = 33.33...%
Practical Applications of Percentage Calculations
Percentage calculations have numerous real-world applications, including:
- Sales and Discounts: Calculating discounts on items during sales events. For example, a 20% discount on a $50 item would be a savings of $10.
- Taxes: Calculating sales tax or income tax. A 6% sales tax on a $100 purchase would be $6.
- Tips: Calculating a tip at a restaurant. A 15% tip on a $40 meal would be $6.
- Interest Rates: Understanding interest earned on savings accounts or interest paid on loans.
- Financial Analysis: Analyzing financial statements and evaluating investment performance. Return on Investment (ROI) calculations heavily rely on percentages.
- Statistics and Data Analysis: Representing proportions and changes in data sets using percentages. For example, understanding survey results or changes in market share.
- Grade Calculation: Determining your final grade in a class, based on individual assignment percentages.
Advanced Percentage Problems and Solutions
Let's explore some more complex percentage problems:
Problem 1: If 25% of a number is 15, what is the number?
Solution:
Let the number be 'x'. We can set up the equation:
0.25x = 15
x = 15 / 0.25 = 60
Therefore, the number is 60.
Problem 2: A price increased by 15% to $69. What was the original price?
Solution:
Let the original price be 'x'. The increased price is 115% of the original price (100% + 15%). We can set up the equation:
1.15x = 69
x = 69 / 1.15 = 60
Therefore, the original price was $60.
Problem 3: What percentage increase is there from 50 to 75?
Solution:
The increase is 75 - 50 = 25. The percentage increase is calculated as:
(Increase / Original Value) * 100 = Percentage Increase
(25 / 50) * 100 = 50%
Therefore, there is a 50% increase from 50 to 75.
Troubleshooting Common Mistakes in Percentage Calculations
Common errors in percentage calculations often stem from:
- Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS).
- Confusing percentage increase/decrease: Understand the difference between finding a percentage of a number and finding the percentage increase or decrease between two numbers.
- Incorrect decimal placement: Ensure you correctly convert decimals to percentages and vice versa.
- Rounding errors: Be aware of rounding errors, especially when dealing with repeating decimals. It's best practice to carry as many decimal places as possible during calculations and round only at the final step.
Resources for Further Learning
Numerous online resources are available to enhance your understanding of percentages. Search for "percentage calculator," "percentage worksheets," or "percentage problems and solutions" to find interactive calculators, practice exercises, and explanatory videos. Many educational websites and YouTube channels offer comprehensive tutorials on the subject.
In conclusion, understanding percentages is essential for navigating various aspects of life. By mastering the techniques outlined in this article, you can confidently tackle percentage problems, from simple calculations like "10 is what percent of 30?" to more complex scenarios involving percentage increases, decreases, and applications in various fields. Remember to practice regularly to solidify your skills and always double-check your work to avoid common errors.
Latest Posts
Latest Posts
-
How Many Ounces Is 10 Cups Of Water
Apr 26, 2025
-
Least Common Factor Of 18 And 30
Apr 26, 2025
-
What Is 6 5 Cm In Mm
Apr 26, 2025
-
Cuanto Es 6 Pies En Metro
Apr 26, 2025
-
What Percent Is 2 Of 9
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about 10 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.