10 Out Of 17 As A Percentage
Kalali
Apr 27, 2025 · 5 min read
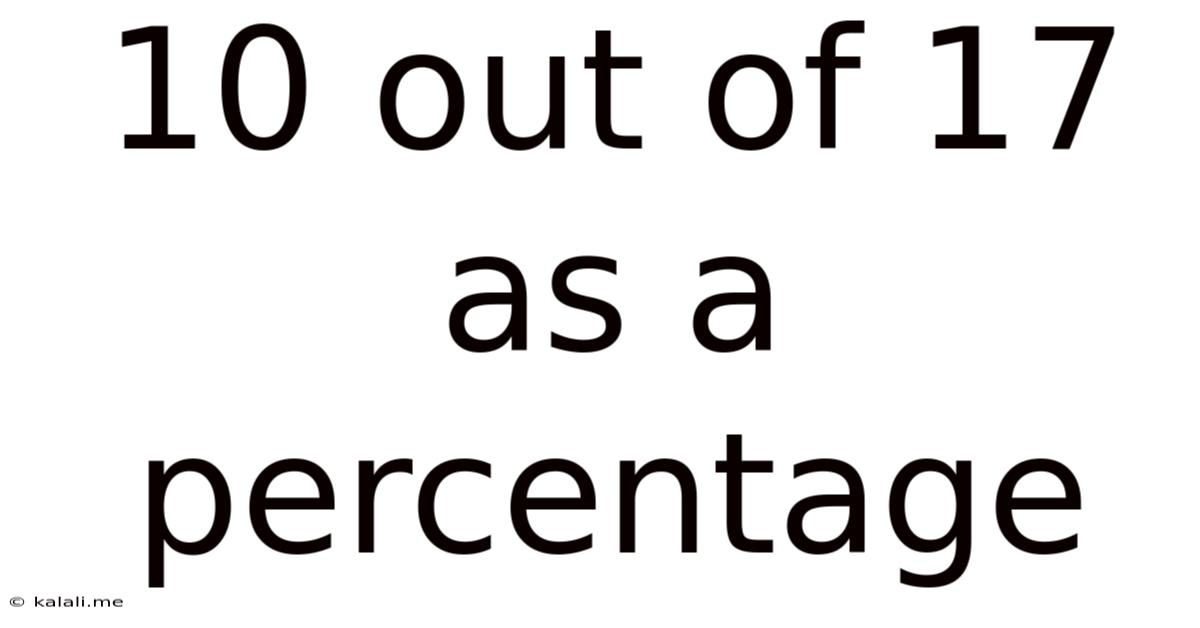
Table of Contents
Decoding Percentages: Understanding 10 out of 17 as a Percentage and its Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments to financial analysis and everyday decision-making. Understanding how to convert fractions into percentages is crucial for interpreting data, making comparisons, and drawing informed conclusions. This article delves into the specifics of calculating "10 out of 17 as a percentage," exploring the method, its applications, and the broader context of percentage calculations.
Meta Description: Learn how to calculate 10 out of 17 as a percentage, understand the underlying principles, and explore real-world applications of percentage calculations in various fields. This comprehensive guide covers the step-by-step process and offers practical examples.
Understanding the Basics of Percentages
A percentage represents a fraction of 100. It's a way of expressing a proportion or ratio as a fraction of 100. The symbol "%" signifies "per cent" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental relationship is crucial for calculating any percentage.
Calculating 10 out of 17 as a Percentage: A Step-by-Step Guide
To calculate 10 out of 17 as a percentage, we follow these simple steps:
-
Express the fraction: First, represent the given information as a fraction. In this case, it's 10/17. This means 10 parts out of a total of 17 parts.
-
Convert the fraction to a decimal: Divide the numerator (10) by the denominator (17): 10 ÷ 17 ≈ 0.5882
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.5882 x 100 ≈ 58.82%
Therefore, 10 out of 17 is approximately 58.82%.
Rounding Percentages
Depending on the context, you might need to round the percentage to a specific number of decimal places. For instance, 58.82% could be rounded to 58.8% or even 59% depending on the required level of precision. Rounding should be done thoughtfully, considering the implications of any loss of accuracy. In many cases, rounding to one decimal place (58.8%) offers a good balance between precision and simplicity.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in numerous fields. Here are some examples demonstrating their diverse applications:
1. Academic Performance:
-
Grade Calculation: Many educational systems use percentages to represent student performance on tests and assignments. For example, if a student answers 10 out of 17 questions correctly on a quiz, their score is 58.82%.
-
Grade Point Average (GPA): GPA calculations often involve converting letter grades into percentage equivalents, which are then averaged to determine the overall GPA.
2. Financial Calculations:
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages.
-
Discounts and Sales: Retail stores commonly advertise discounts as percentages (e.g., a 20% discount).
-
Tax Calculations: Sales tax, income tax, and other taxes are frequently calculated as a percentage of the total amount.
-
Profit Margins: Businesses use percentage calculations to determine their profit margins—the difference between revenue and cost, expressed as a percentage of revenue.
3. Data Analysis and Statistics:
-
Statistical Data Representation: Percentages are frequently used to represent proportions and trends within datasets. For example, the percentage of a population with a particular characteristic or the percentage change in a variable over time.
-
Probability and Risk Assessment: Percentages are crucial in expressing probabilities and assessing risk in various scenarios. For instance, the likelihood of a specific event occurring might be expressed as a percentage.
4. Everyday Life:
-
Tip Calculations: Calculating tips in restaurants often involves determining a percentage of the total bill.
-
Recipe Adjustments: Scaling recipes up or down requires adjusting ingredient quantities proportionally, which often involves percentage calculations.
5. Scientific and Engineering Applications:
-
Measurement Errors: Percentage errors are used to quantify the uncertainty or error in measurements.
-
Efficiency Calculations: The efficiency of machines and processes is often expressed as a percentage.
Advanced Percentage Calculations: Beyond the Basics
While calculating 10 out of 17 as a percentage is straightforward, more complex scenarios might involve multiple steps or the need to work backward from a percentage to find an original value.
1. Finding the Original Value from a Percentage:
Let's say a product is discounted by 25%, and its sale price is $60. To find the original price, we can use the following approach:
-
The sale price represents 75% (100% - 25%) of the original price.
-
Let 'x' be the original price. Then, 0.75x = $60
-
Solving for x: x = $60 / 0.75 = $80
Therefore, the original price was $80.
2. Percentage Change Calculations:
Percentage change calculations are frequently used to compare values over time or across different groups. The formula is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a company's revenue increased from $100,000 to $120,000, the percentage change is:
[(120,000 - 100,000) / 100,000] x 100% = 20%
The revenue increased by 20%.
Mastering Percentage Calculations: Tips and Techniques
To improve your proficiency in percentage calculations, consider these tips:
-
Practice Regularly: The more you practice, the more comfortable you will become with the concepts and techniques.
-
Use Calculators Effectively: Calculators can significantly streamline the process, especially for complex calculations.
-
Understand the Underlying Concepts: Focus on grasping the fundamental principles rather than just memorizing formulas.
-
Break Down Complex Problems: Divide complex percentage problems into smaller, more manageable steps.
-
Check Your Work: Always double-check your calculations to ensure accuracy.
Conclusion: The Importance of Percentage Understanding
The ability to calculate and interpret percentages is a valuable skill that extends far beyond the classroom. From managing personal finances to analyzing data and making informed decisions in various professional settings, a solid understanding of percentages is essential for navigating the complexities of the modern world. Mastering percentage calculations empowers you to interpret information critically, solve problems effectively, and make more informed choices in all aspects of your life. This guide serves as a foundation for building this crucial skill, equipping you with the knowledge and techniques to confidently tackle percentage-related challenges.
Latest Posts
Latest Posts
-
How Many Ounces Is 1 4 Pound
Apr 27, 2025
-
How Many Inches In 81 Cm
Apr 27, 2025
-
What Is 4 10 As A Decimal
Apr 27, 2025
-
29 Cm In Inches And Feet
Apr 27, 2025
-
How Much Is 5 Minutes In Seconds
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 17 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.