10 Times As Much As 100 Is
Kalali
Jul 18, 2025 · 6 min read
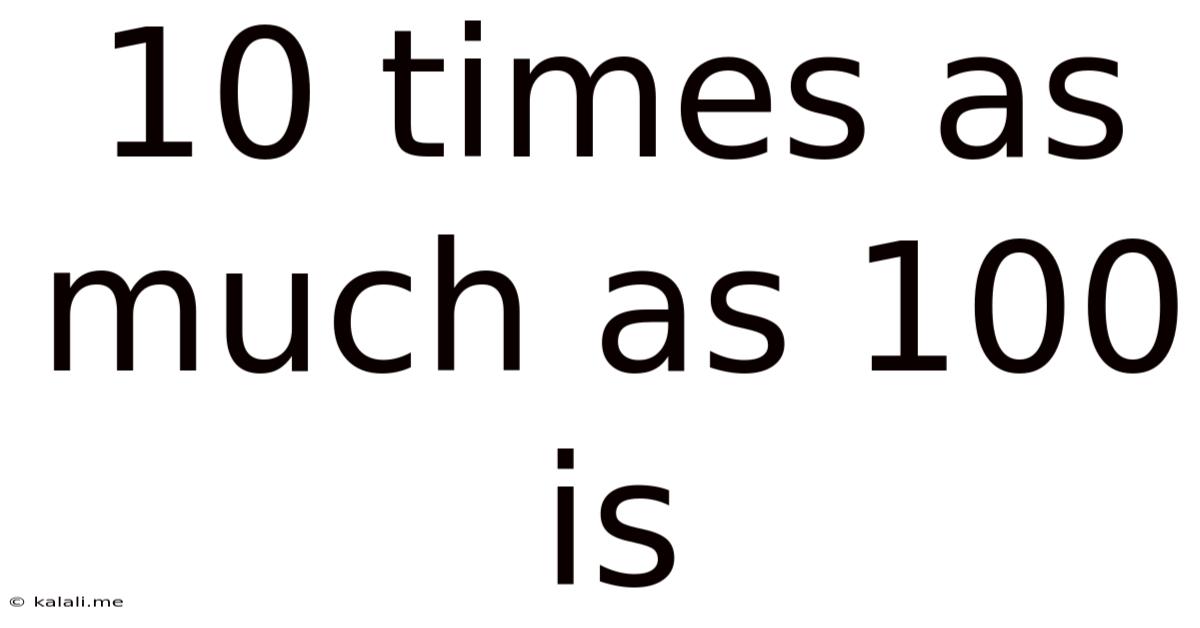
Table of Contents
10 Times as Much as 100 Is: Exploring Multiplication and its Applications
This seemingly simple question, "10 times as much as 100 is?", opens the door to a fascinating exploration of multiplication, its practical applications, and its role in understanding the world around us. At its core, the answer is straightforward: 10 multiplied by 100 equals 1000. However, delving deeper reveals the broader significance of this fundamental mathematical operation and its impact on various fields. This article will unpack this seemingly simple calculation, examining its implications in diverse contexts, from everyday life to complex scientific calculations.
Understanding Multiplication: The Foundation of 10 x 100
Multiplication is essentially repeated addition. When we say "10 times as much as 100," we're asking for the result of adding 100 to itself ten times. This can be represented as: 100 + 100 + 100 + 100 + 100 + 100 + 100 + 100 + 100 + 100 = 1000. However, multiplication provides a far more efficient way to express and calculate this sum. The equation 10 x 100 = 1000 concisely captures the same operation.
This understanding forms the basis for solving similar problems. For instance, if the question was "5 times as much as 250 is?", we would simply multiply 5 by 250, resulting in 1250. The principle remains consistent: repeated addition, efficiently represented through multiplication.
The Commutative Property and its Significance
Multiplication possesses a crucial property known as the commutative property. This means that the order of the numbers being multiplied doesn't affect the outcome. Therefore, 10 x 100 is identical to 100 x 10, both equaling 1000. This seemingly minor detail holds significant practical implications, enabling flexibility in problem-solving and simplifying complex calculations.
Applications of Multiplication: Beyond the Basics
The simple equation, 10 x 100 = 1000, isn't just an abstract mathematical concept; it has far-reaching applications across numerous disciplines. Let's delve into some key examples:
1. Everyday Finances:
- Calculating total costs: Imagine buying 10 items priced at $100 each. The total cost is easily determined using multiplication: 10 x $100 = $1000. This applies to various scenarios, from grocery shopping to larger purchases.
- Calculating earnings: If you earn $100 per day for 10 days, your total earnings are 10 x $100 = $1000.
- Budgeting: Multiplication helps in budgeting by quickly estimating the cost of multiple expenses. For instance, if you need 100 gallons of paint at $10 per gallon, the total cost is 100 x $10 = $1000.
2. Measurement and Conversion:
- Unit conversions: Multiplication plays a critical role in converting units. For example, converting 10 kilometers to meters involves multiplying by 1000 (since there are 1000 meters in a kilometer): 10 km x 1000 m/km = 10,000 meters.
- Calculating area: To find the area of a rectangle, you multiply its length by its width. If a rectangle measures 10 meters by 100 meters, its area is 10 x 100 = 1000 square meters.
- Calculating volume: Similarly, calculating the volume of a rectangular prism requires multiplying length, width, and height.
3. Scientific Applications:
- Physics: Numerous physics formulas rely on multiplication. Calculating work done (force x distance), kinetic energy (1/2 x mass x velocity²), or momentum (mass x velocity) all necessitate multiplication.
- Chemistry: Stoichiometry, the study of quantitative relationships in chemical reactions, extensively uses multiplication to calculate the amounts of reactants and products.
- Engineering: Engineering designs involve countless calculations utilizing multiplication, from structural analysis to fluid dynamics.
4. Data Analysis and Statistics:
- Calculating averages: While averages often involve division, multiplication is used in calculating weighted averages where different data points have varying levels of importance.
- Scaling data: In data analysis, multiplication is used to scale data to a different range or adjust for factors like inflation.
5. Computer Science:
- Image processing: Image manipulation often involves multiplying pixel values to adjust brightness, contrast, or color saturation.
- Algorithm design: Numerous algorithms utilize multiplication for operations such as matrix multiplication or performing fast Fourier transforms.
Expanding the Concept: Beyond Simple Multiplication
The question "10 times as much as 100 is" can be expanded to explore more complex mathematical concepts:
1. Percentages: Calculating 10% of 1000 involves multiplying 1000 by 0.1 (10/100), resulting in 100. Understanding percentages builds upon the foundation of multiplication.
2. Exponents: Raising 10 to the power of 3 (10³) means multiplying 10 by itself three times: 10 x 10 x 10 = 1000. Exponents represent repeated multiplication.
3. Scientific Notation: Large numbers like 1000 can be expressed in scientific notation as 1 x 10³. This notation is crucial in fields like physics and astronomy for handling extremely large or small numbers.
4. Algebra: Algebraic equations frequently involve multiplication. For example, solving the equation 10x = 1000 involves dividing both sides by 10, demonstrating the inverse relationship between multiplication and division.
Real-World Examples Illustrating 10 x 100 = 1000
Let's look at some concrete examples to show how the multiplication we've discussed applies in practical scenarios:
-
A school fundraiser: A school aims to raise $1000 for new sports equipment. If they have 10 different fundraising events, each event needs to generate $100 (1000 / 10 = 100). Conversely, if each event generates $100, and they have 10 events, they achieve their $1000 goal (10 x 100 = 1000).
-
Construction project: A contractor needs 1000 bricks to complete a wall. If each pallet contains 100 bricks, they need to order 10 pallets (1000 / 100 = 10). Alternatively, if they order 10 pallets of 100 bricks each, they'll have 1000 bricks (10 x 100 = 1000).
-
Inventory Management: A warehouse has 100 boxes of a particular item. Each box contains 10 units. The total inventory is 1000 units (100 x 10 = 1000).
-
Investment Growth: If an investment grows by 10% annually, and the initial investment is $1000, the growth in the first year would be 10% of $1000, or $100 ($1000 x 0.10 = $100).
These examples highlight the ubiquity of multiplication in our daily lives, often without us explicitly recognizing it. The seemingly simple equation, 10 x 100 = 1000, serves as a foundation for more complex calculations and problem-solving across various domains.
Conclusion: The Enduring Importance of Multiplication
The answer to "10 times as much as 100 is" is 1000. However, the significance of this answer extends far beyond the simple arithmetic. Understanding multiplication is fundamental to numeracy, empowering individuals to tackle practical problems in finance, measurement, science, and technology. The commutative property adds flexibility, while the concept's expansion into percentages, exponents, and algebraic equations demonstrates its far-reaching implications within mathematics. Ultimately, the ability to confidently and efficiently perform multiplication is a crucial skill that enhances problem-solving capabilities and contributes to a deeper comprehension of the world around us. From everyday transactions to complex scientific calculations, multiplication remains an indispensable tool in navigating and understanding our quantitative reality.
Latest Posts
Latest Posts
-
What Does It Mean When It Asks For Your Title
Jul 18, 2025
-
What Fruit Does Santas Nose Look Like
Jul 18, 2025
-
Did You Hear About Math Worksheet Answers
Jul 18, 2025
-
Is Electricity An Element Compound Or Mixture
Jul 18, 2025
-
How Many 750 Ml Bottles In A 1 75 Liter
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about 10 Times As Much As 100 Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.