10 To The Negative 2 Power
Kalali
Apr 04, 2025 · 4 min read
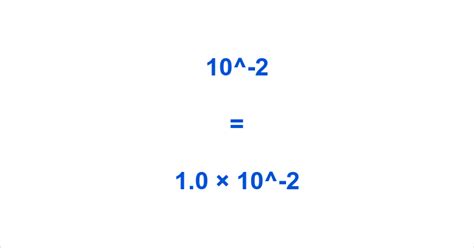
Table of Contents
10 to the Negative 2 Power: A Deep Dive into Scientific Notation and its Applications
Understanding exponents, especially negative exponents, is crucial for anyone working with scientific notation, engineering, or any field dealing with very large or very small numbers. This article provides a comprehensive exploration of 10 to the negative 2 power (10⁻²), explaining its meaning, calculation, real-world applications, and its significance within the broader context of scientific notation and exponential math.
What Does 10⁻² Mean?
At its core, 10⁻² represents 10 raised to the power of -2. In simpler terms, it's a way of expressing a fraction where the numerator is 1 and the denominator is 10² (10 squared, or 10 multiplied by itself). Mathematically, this can be written as:
10⁻² = 1 / 10² = 1 / (10 x 10) = 1/100 = 0.01
Understanding Negative Exponents
The negative exponent signifies a reciprocal. Remember the rule of exponents: a⁻ⁿ = 1/aⁿ. This rule holds true for any base (a) and any exponent (n). In our case, a = 10 and n = 2. Therefore, 10⁻² is the reciprocal of 10².
Calculating 10⁻²: A Step-by-Step Guide
Calculating 10⁻² is straightforward:
- Identify the base and the exponent: The base is 10, and the exponent is -2.
- Apply the reciprocal rule: Since the exponent is negative, we take the reciprocal of 10 raised to the positive power. This means we calculate 1/10².
- Calculate 10²: 10² = 10 x 10 = 100
- Calculate the reciprocal: 1/100 = 0.01
Therefore, 10⁻² = 0.01
The Significance of Scientific Notation
Scientific notation is a crucial tool for representing extremely large or extremely small numbers concisely and efficiently. It uses the form a x 10ⁿ, where 'a' is a number between 1 and 10 (but not including 10), and 'n' is an integer exponent. 10⁻² serves as a fundamental building block in this system, allowing us to represent numbers in the hundredths place and beyond conveniently.
Examples of Scientific Notation using 10⁻²
- 0.01 meters: This can be expressed as 1 x 10⁻² meters, representing one centimeter.
- 0.01 seconds: This is equivalent to 1 x 10⁻² seconds, or ten milliseconds.
- 0.01 grams: This represents 1 x 10⁻² grams, or ten milligrams.
Real-world Applications of 10⁻²
The application of 10⁻² extends across various fields:
1. Physics and Engineering
- Measurement of length: As previously mentioned, 10⁻² meters represents one centimeter, a commonly used unit in many measurements.
- Electrical Engineering: 10⁻² is frequently used in representing electrical quantities such as capacitance (farads) and inductance (henries).
- Mechanics: Calculations involving force, work, and energy often involve quantities expressed using powers of 10, including 10⁻².
2. Chemistry
- Molarity: In chemistry, molarity (moles per liter) often results in values requiring scientific notation, frequently utilizing 10⁻² and other negative exponents.
- Concentration of solutions: Expressing the concentration of dilute solutions frequently employs 10⁻², and similar terms.
3. Biology and Medicine
- Microscopic measurements: Measuring the sizes of cells and microorganisms often involves units smaller than a millimeter, leading to the use of 10⁻² and even smaller powers of 10.
- Dosage calculations: Pharmaceutical calculations often involve extremely small quantities, necessitating the use of scientific notation, frequently including terms like 10⁻².
4. Computer Science
- Data representation: Computers use binary systems, but the interpretation and representation of data often involve powers of 10, including 10⁻², particularly when dealing with decimal approximations.
Expanding on Negative Exponents
Understanding 10⁻² allows for a broader grasp of negative exponents in general. The principles apply to any base, not just 10. For example:
- 2⁻² = 1/2² = 1/4 = 0.25
- 5⁻² = 1/5² = 1/25 = 0.04
The reciprocal rule remains consistent regardless of the base.
Connecting 10⁻² to Other Powers of 10
It's beneficial to understand how 10⁻² relates to other powers of 10:
- 10⁰ = 1 (Anything raised to the power of 0 is 1)
- 10¹ = 10
- 10² = 100
- 10⁻¹ = 0.1
- 10⁻² = 0.01
- 10⁻³ = 0.001
This sequence illustrates the pattern of decreasing values as the negative exponent increases (in magnitude).
Practical Exercises
To solidify your understanding of 10⁻², try these exercises:
- Convert the following to scientific notation: 0.005 meters, 0.00025 kilograms, 0.08 seconds.
- Convert the following from scientific notation to decimal form: 3 x 10⁻² grams, 7 x 10⁻³ liters, 2.5 x 10⁻² meters.
- Calculate: (2 x 10⁻²) + (5 x 10⁻²)
- Explain the difference between 10⁻² and 10².
Conclusion: The Ubiquity of 10⁻²
10⁻² (or 0.01) might seem like a simple concept, but its significance in representing small quantities within the framework of scientific notation is immense. Its applications span numerous scientific and engineering disciplines, emphasizing the importance of understanding exponents and the power of scientific notation for clear and efficient communication of numerical data. Mastering this concept will undoubtedly enhance your proficiency in various quantitative fields. By grasping the principles outlined in this article, you will be better equipped to handle complex calculations and effectively interpret scientific information involving small quantities. Remember to practice using this knowledge regularly to fully absorb its application.
Latest Posts
Latest Posts
-
58 Inches Is How Many Feet
Apr 04, 2025
-
How Many Cups Is 64 Ounces Of Water
Apr 04, 2025
-
How Many Inches In 13 5 Cm
Apr 04, 2025
-
Is 13 A Prime Number Or Composite
Apr 04, 2025
-
What Percentage Of Y Is X
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 10 To The Negative 2 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
