10 To The Power Of Negative 3
Kalali
May 10, 2025 · 2 min read
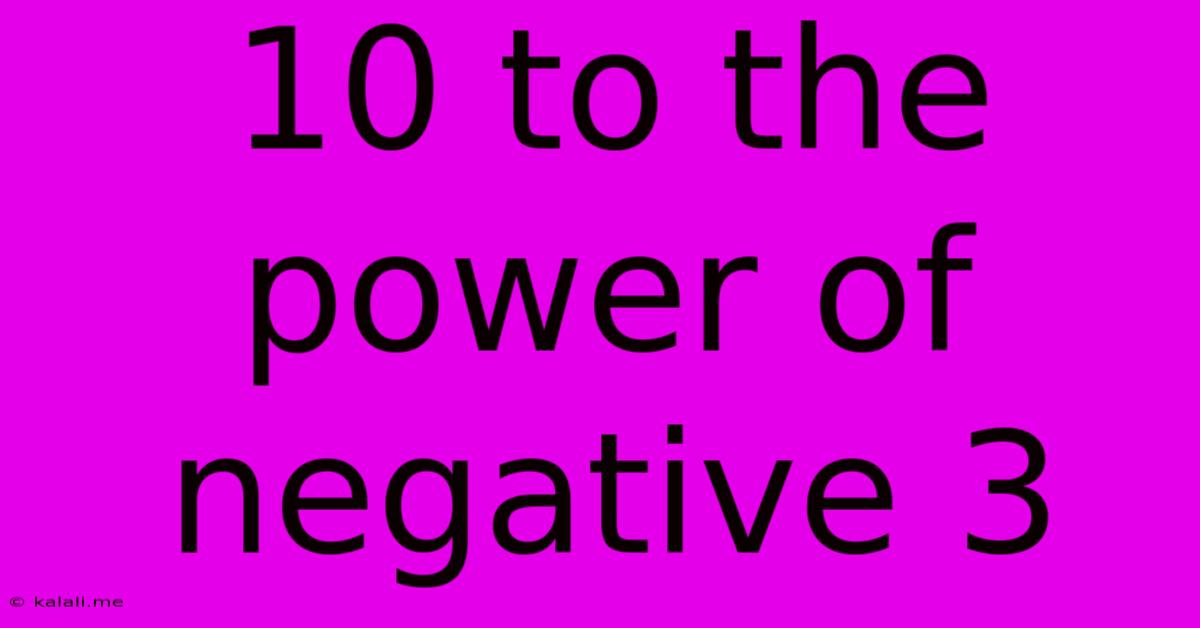
Table of Contents
Understanding 10 to the Power of Negative 3 (10⁻³)
This article will demystify the seemingly complex concept of 10 to the power of negative 3 (10⁻³), explaining what it means, how to calculate it, and its practical applications in various fields. Understanding this fundamental concept is crucial for anyone working with scientific notation, measurements, and data analysis.
What does 10⁻³ mean?
In mathematics, 10⁻³ represents a number expressed in scientific notation. It signifies one tenth raised to the power of three, or, more simply, one thousandth. This is equivalent to 1/1000 or 0.001. The negative exponent indicates a reciprocal; it's the inverse of 10³. Understanding exponents and their application to the base number 10 is key to grasping scientific notation and its uses in various disciplines.
Calculating 10⁻³:
The calculation is straightforward:
10⁻³ = 1 / 10³ = 1 / (10 * 10 * 10) = 1 / 1000 = 0.001
Therefore, 10⁻³ is equal to 0.001. This simple calculation forms the foundation for understanding more complex scientific notations involving negative exponents.
Practical Applications of 10⁻³:
The application of 10⁻³ extends to various fields, particularly those involving small measurements:
-
Metric System: 10⁻³ is a common factor in the metric system. It represents the prefix "milli," denoting one-thousandth of a unit. For example:
- Millimeter (mm): 1 mm = 10⁻³ meters (m)
- Milliliter (ml): 1 ml = 10⁻³ liters (l)
- Milligram (mg): 1 mg = 10⁻³ grams (g)
-
Scientific Notation: In science, 10⁻³ is frequently used to express very small numbers concisely. This simplifies writing and manipulating extremely small values encountered in fields like chemistry, physics, and engineering.
-
Data Analysis: When dealing with datasets containing very small numbers, converting them to scientific notation using 10⁻³ (or other negative powers of 10) improves readability and data management.
-
Computer Science: In computer science and digital systems, binary representations often involve powers of two, but understanding decimal equivalents using powers of ten is equally vital for data conversion and calculations.
Understanding Negative Exponents:
The concept of negative exponents is integral to understanding 10⁻³. Remember that a negative exponent simply indicates the reciprocal of the positive exponent. For any base number 'a' and exponent 'n', a⁻ⁿ = 1 / aⁿ. This rule applies universally and is essential for working with scientific notation and various mathematical problems.
Conclusion:
10⁻³ (or one thousandth) is a fundamental concept with widespread practical applications. Understanding its meaning, calculation, and uses in various fields is crucial for anyone working with numerical data or scientific notation. By grasping this concept, you'll gain a solid foundation for tackling more complex mathematical problems and enhancing your comprehension of scientific concepts. This simple yet powerful concept unlocks a deeper understanding of the world around us, represented in everything from microscopic measurements to vast astronomical distances.
Latest Posts
Latest Posts
-
The Ability To Say Clever And Funny Things
Jun 30, 2025
-
How Many Cups Are In A Pound Of Lard
Jun 30, 2025
-
Why Did Jerry Thompson And Kelly Nelon Divorce
Jun 30, 2025
-
Allen And Roth Patio Furniture Replacement Parts
Jun 30, 2025
-
How Many Minutes Are In 20 Miles
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about 10 To The Power Of Negative 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.