107 Out Of 150 As A Percentage
Kalali
Apr 01, 2025 · 5 min read
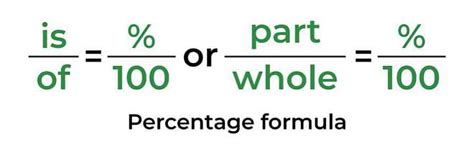
Table of Contents
107 out of 150 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with applications spanning various fields, from academic assessments to financial transactions and data analysis. Understanding how to convert fractions into percentages is crucial for interpreting data and making informed decisions. This article provides a detailed explanation of how to calculate 107 out of 150 as a percentage, along with a broader exploration of percentage calculations and their practical uses. We will delve into the process, explore different methods, and discuss the significance of accuracy in percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100". Therefore, 10% represents 10 out of 100, 50% represents 50 out of 100, and so on. Percentages are widely used because they provide a standardized way to compare proportions and make data easily understandable.
Calculating 107 out of 150 as a Percentage: The Basic Method
The most straightforward way to calculate the percentage is using a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 107 (the number you're interested in)
- Whole: 150 (the total number)
Substituting these values into the formula:
(107 / 150) * 100% = 71.333...%
Therefore, 107 out of 150 is approximately 71.33%. We typically round percentages to two decimal places for clarity.
Alternative Methods for Calculating Percentages
While the above method is the most common, there are other approaches you can use:
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 107 ÷ 150 =, then multiply by 100. The calculator will automatically display the percentage.
-
Using Spreadsheet Software: Programs like Microsoft Excel or Google Sheets have built-in functions for percentage calculations. You can use the formula
=(107/150)*100in a cell to obtain the result.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in a wide array of contexts:
-
Academic Performance: Students often need to calculate their grades based on the number of questions answered correctly out of the total number of questions. For example, a student scoring 107 out of 150 on an exam achieves a score of 71.33%.
-
Financial Calculations: Percentages are essential in finance for calculating interest rates, discounts, profits, losses, and tax rates. Understanding percentage changes is vital for monitoring investments and making financial decisions. For instance, if a stock price increases from $100 to $107, it has increased by 7%.
-
Data Analysis: Percentages are used extensively in data analysis to represent proportions, trends, and comparisons. For example, in market research, percentages can show the proportion of consumers who prefer a particular product.
-
Statistics and Probability: Percentages play a significant role in statistics and probability calculations. For instance, the probability of an event occurring can be expressed as a percentage.
-
Everyday Life: Calculating percentages is useful in various everyday situations, such as determining tips in restaurants, calculating discounts in stores, and understanding sales tax.
Importance of Accuracy in Percentage Calculations
Accuracy in percentage calculations is paramount, especially in situations with financial or scientific implications. Rounding errors can lead to significant inaccuracies, especially when dealing with large numbers or complex calculations. It's crucial to use appropriate rounding techniques and to maintain accuracy throughout the calculation process. For instance, if you're calculating a discount on a large purchase, a small error in the percentage calculation can result in a considerable difference in the final price.
Beyond the Basics: Understanding Percentage Increase and Decrease
The calculation of 107 out of 150 is a straightforward example of calculating a percentage of a whole. However, it's equally important to understand how to calculate percentage increase or decrease.
Let's say a value increases from an initial value (A) to a final value (B). The percentage increase is calculated as:
[(B - A) / A] * 100%
Similarly, if a value decreases from an initial value (A) to a final value (B), the percentage decrease is calculated as:
[(A - B) / A] * 100%
These calculations are essential for tracking changes in various metrics such as sales figures, population growth, or stock prices.
Advanced Applications: Compounding Percentages
In situations involving repeated percentage changes, such as compound interest calculations, the compounding effect must be considered. This means that each subsequent percentage change is applied to the new value, not the original value. For example, if an investment grows by 10% in year one and 15% in year two, the final value is not simply a sum of the percentage increases. Instead, the calculations would be performed sequentially, taking the compounded effect into account.
Error Analysis and Avoiding Common Mistakes
When calculating percentages, several common mistakes can occur:
-
Incorrect Formula: Using the wrong formula or placing values incorrectly in the formula can lead to wrong answers. Double-checking the formula is essential to avoid this.
-
Rounding Errors: Rounding intermediate results can cause cumulative errors, especially in complex calculations. It's best practice to keep as many decimal places as possible throughout the calculation, only rounding the final result.
-
Misinterpretation of the Problem: Carefully read and understand the problem statement to accurately identify the "part" and the "whole." Misinterpreting the problem can lead to incorrect calculations.
Conclusion: Mastering Percentage Calculations
Calculating 107 out of 150 as a percentage, while seemingly simple, illustrates the foundational importance of understanding percentage calculations. This skill extends far beyond basic arithmetic, impacting numerous aspects of daily life, academic pursuits, and professional fields. Mastering percentage calculations, including understanding percentage increases and decreases and the implications of compounding, is essential for making informed decisions and interpreting data accurately. By consistently using the correct formulas, paying attention to accuracy, and understanding the various applications of percentage calculations, one can greatly enhance their analytical skills and problem-solving capabilities. The ability to confidently and accurately calculate percentages is a valuable asset in both personal and professional life.
Latest Posts
Latest Posts
-
A Toy Rocket Is Launched Vertically From Ground Level
Apr 02, 2025
-
50 30 Written As A Product Of Two Factors
Apr 02, 2025
-
What Percentage Is 11 Out Of 12
Apr 02, 2025
-
How Many Fahrenheit Is 1 Degree Celsius
Apr 02, 2025
-
What Percent Of 6 Is 4
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 107 Out Of 150 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
