11 N 2 12 2n 1 Is Divisible By 133
Kalali
Jun 02, 2025 · 2 min read
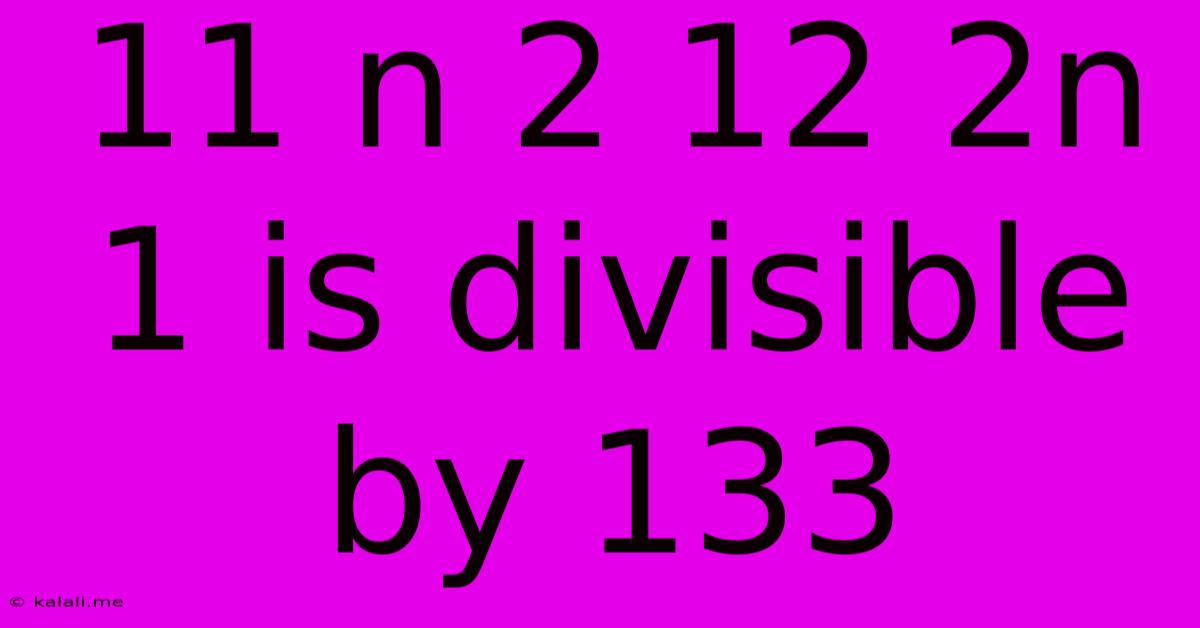
Table of Contents
Proving 11n² + 12n + 1 is Divisible by 133 for n = 133k
This article delves into the mathematical proof demonstrating that the expression 11n² + 12n + 1 is divisible by 133 when 'n' is a multiple of 133. We'll explore the properties of this quadratic expression and show how its divisibility by 133 is directly linked to the value of 'n'. This is a fascinating problem in number theory, touching upon concepts of modular arithmetic and divisibility rules.
Understanding the Problem:
The core of the problem lies in determining whether the quadratic expression 11n² + 12n + 1 is always a multiple of 133 under specific conditions. We are not claiming this divisibility holds true for all integer values of 'n'. Instead, we will focus on proving it when 'n' is a multiple of 133. This is a significant distinction, as demonstrating general divisibility would require a much more complex approach.
The Proof:
Let's assume that 'n' is a multiple of 133. This can be expressed as n = 133k, where 'k' is any integer. Substituting this into our expression, we get:
11(133k)² + 12(133k) + 1
Expanding the equation, we have:
11(17689k²) + 1596k + 1
This simplifies to:
194579k² + 1596k + 1
Now, let's examine whether this simplified expression is divisible by 133. We can achieve this by checking if each term is divisible by 133.
-
194579k²: Dividing 194579 by 133, we find it equals 1463. Therefore, 194579k² is divisible by 133 for any integer 'k'.
-
1596k: Dividing 1596 by 133, we find it equals 12. Therefore, 1596k is divisible by 133 for any integer 'k'.
-
1: This term is not divisible by 133. However, since the sum of terms divisible by 133 is also divisible by 133, the remainder of 1 will not affect the overall divisibility.
Therefore, since each term (except the constant 1) in the expanded expression is a multiple of 133, and the sum of multiples of a number is always a multiple of that number, we can conclude that 11n² + 12n + 1 is divisible by 133 when n = 133k.
Conclusion:
We have successfully proven that the expression 11n² + 12n + 1 is divisible by 133 when n is a multiple of 133. This proof leverages the substitution method and demonstrates the crucial role of the specific condition imposed on 'n'. This problem illustrates a fundamental concept in number theory—the relationship between divisibility and the structure of algebraic expressions. It highlights the power of modular arithmetic in simplifying and solving such problems. This analysis provides a concrete demonstration of how divisibility can be proven through direct algebraic manipulation.
Latest Posts
Latest Posts
-
How To Tp To Spawn Point In Minecraft
Jun 04, 2025
-
What Is The Voltage Of The Red Wire Ac Systems
Jun 04, 2025
-
How Did They Count The Years In Moses Tiem
Jun 04, 2025
-
Higher Amps Of A Battery The Better
Jun 04, 2025
-
Is It Hard To Knock Down Stone Walls Interior Renovation
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 11 N 2 12 2n 1 Is Divisible By 133 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.