12 Is 30 Of What Number
Kalali
Apr 06, 2025 · 4 min read
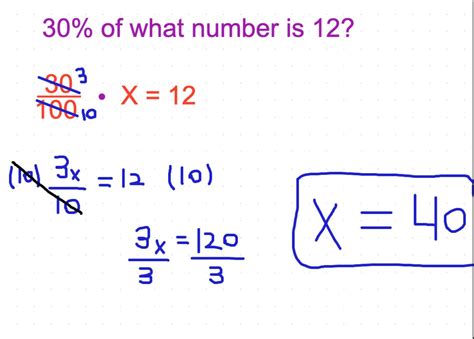
Table of Contents
12 is 30% of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial reports. This article will delve into the question, "12 is 30% of what number?", providing a step-by-step solution, exploring different approaches, and offering practical examples to solidify your understanding of percentage calculations. We'll also explore the broader context of percentage problems and how to tackle similar questions with confidence.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of 100." For example, 30% can be written as 30/100 or 0.30 (as a decimal).
This fundamental understanding allows us to translate percentage problems into algebraic equations that we can solve.
Solving "12 is 30% of What Number?"
Our problem can be expressed as an equation:
12 = 0.30 * x
Where 'x' is the unknown number we need to find.
Method 1: Algebraic Solution
To solve for 'x', we follow these steps:
-
Divide both sides of the equation by 0.30: This isolates 'x' on one side of the equation.
x = 12 / 0.30
-
Perform the division:
x = 40
Therefore, 12 is 30% of 40.
Method 2: Using Proportions
Percentage problems can also be solved using proportions. We can set up a proportion as follows:
12/x = 30/100
This proportion states that the ratio of 12 to the unknown number (x) is equal to the ratio of 30 to 100 (which is the definition of 30%).
To solve this proportion, we can cross-multiply:
12 * 100 = 30 * x
1200 = 30x
Now, divide both sides by 30:
x = 1200 / 30
x = 40
Again, we arrive at the solution: x = 40.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial for various aspects of daily life. Let's explore some real-world scenarios where this type of problem might arise:
1. Sales and Discounts: A store offers a 30% discount on an item. The discounted price is $12. What was the original price? This is exactly the same problem we just solved – the original price was $40.
2. Taxes: You paid $12 in sales tax, and the tax rate is 30%. What was the pre-tax price of your purchase? This again translates to the same equation, yielding a pre-tax price of $40.
3. Commission: A salesperson earned a 30% commission on a sale. The commission amount was $12. What was the total value of the sale? The solution remains the same: the total sale value was $40.
4. Surveys and Statistics: In a survey, 30% of respondents answered "yes" to a particular question. If 12 people answered "yes," how many people participated in the survey in total? This mirrors the problem, resulting in a total of 40 survey participants.
Extending the Concept: Variations on Percentage Problems
The fundamental approach we used can be adapted to solve various percentage problems. Let's look at a few variations:
1. Finding the Percentage: What percentage of 40 is 12?
To solve this, we set up the equation:
x/100 * 40 = 12
Solving for x (by dividing both sides by 40 and then multiplying by 100), we get x = 30%.
2. Finding the Whole Number: 15 is 25% of what number?
Following the same method as before:
15 = 0.25 * x
x = 15 / 0.25
x = 60
Therefore, 15 is 25% of 60.
3. Percentage Increase/Decrease: A price increased by 30% to reach $52. What was the original price?
Let 'x' be the original price. Then:
x + 0.30x = 52
1.30x = 52
x = 52 / 1.30
x = 40
The original price was $40.
Tips and Tricks for Solving Percentage Problems
- Convert percentages to decimals: This simplifies calculations.
- Use proportions: This method is particularly helpful for visualizing the relationship between the different quantities.
- Check your answer: Does the answer make sense in the context of the problem?
- Practice regularly: The more you practice, the more comfortable and efficient you'll become.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems is a valuable skill with wide-ranging practical applications. By understanding the underlying principles and employing the methods outlined in this article, you can confidently tackle various percentage-related problems, from simple calculations to more complex scenarios involving increases and decreases. Remember to practice consistently to build your proficiency and improve your problem-solving skills. The ability to quickly and accurately perform percentage calculations will prove invaluable in many aspects of your personal and professional life. Through consistent practice and application, you can truly master this important mathematical skill.
Latest Posts
Latest Posts
-
What Is 30 Percent Of 15
Apr 07, 2025
-
How Many Inches Is 164 Cm
Apr 07, 2025
-
How Long Is 40 Inches In Cm
Apr 07, 2025
-
12 Cups Equals How Many Quarts
Apr 07, 2025
-
Words With K In The Middle
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about 12 Is 30 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.