12 Is What Percent Of 60
Kalali
Mar 31, 2025 · 5 min read
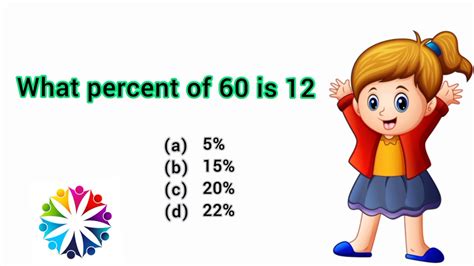
Table of Contents
12 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and budgeting to academic assessments and everyday life. This comprehensive guide will delve into the question, "12 is what percent of 60?", exploring various methods to solve this problem and expanding on the broader concept of percentage calculations. We'll cover different approaches, including the formula method, the proportion method, and using a calculator, providing a detailed explanation suitable for all levels of mathematical understanding.
Understanding Percentages: A Foundation
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% signifies 50 out of 100, which can be simplified to ½ or 0.5. Percentages are a useful way to represent parts of a whole, making comparisons and calculations easier.
Method 1: The Formula Method
This is the most straightforward method for calculating percentages. The basic formula is:
(Part / Whole) x 100% = Percentage
In our problem, "12 is what percent of 60?", we identify:
- Part: 12
- Whole: 60
Applying the formula:
(12 / 60) x 100% = 0.2 x 100% = 20%
Therefore, 12 is 20% of 60.
Step-by-Step Breakdown:
- Identify the Part and the Whole: Clearly define the part (12) and the whole (60) from the problem statement.
- Divide the Part by the Whole: Divide the part (12) by the whole (60). This gives you a decimal value (0.2 in this case).
- Multiply by 100: Multiply the decimal value by 100 to convert it into a percentage.
Method 2: The Proportion Method
This method utilizes the concept of proportions to solve percentage problems. We set up a proportion using two ratios:
- Part / Whole = Percentage / 100
Let's apply this to our problem:
12 / 60 = x / 100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
60x = 1200
x = 1200 / 60
x = 20
Therefore, 12 is 20% of 60.
Step-by-Step Breakdown:
- Set up the Proportion: Create a proportion using the known values and the unknown percentage (x).
- Cross-Multiply: Multiply the numerator of one ratio by the denominator of the other, and vice-versa.
- Solve for x: Isolate the variable 'x' by performing the necessary algebraic operations.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply divide the part (12) by the whole (60), then multiply the result by 100. The calculator will automatically display the answer as a percentage (20%).
This method offers speed and efficiency, especially for more complex calculations. However, understanding the underlying principles (as demonstrated in Methods 1 and 2) is crucial for developing a strong mathematical foundation.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in various real-world scenarios. Here are a few examples:
- Finance: Calculating interest rates, discounts, taxes, and profit margins all rely on percentage calculations. For example, if a store offers a 25% discount on an item, you can use percentages to determine the final price.
- Academics: Grades are often expressed as percentages, reflecting the student's performance relative to the total possible marks.
- Statistics: Percentages are extensively used to represent data and interpret statistical results in surveys, polls, and research studies. For example, understanding market share requires familiarity with percentages.
- Everyday Life: Calculating tips at restaurants, determining sale prices, and comprehending nutritional information on food labels all involve percentage calculations.
Expanding on Percentage Calculations: Further Exploration
Beyond the basic calculations, understanding percentages can involve more complex scenarios:
- Percentage Increase/Decrease: This involves calculating the change in a value relative to its original value. For instance, finding the percentage increase in sales from one year to the next.
- Finding the Original Value: If you know the percentage and the resulting value after a percentage increase or decrease, you can calculate the original value using reverse percentage calculations.
- Compound Percentages: This involves applying a percentage repeatedly over time, often encountered in financial calculations like compound interest.
- Percentage Points: It's crucial to differentiate between percentage change and percentage points. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
Solving More Complex Percentage Problems: Examples
Let's explore a few more complex scenarios to reinforce our understanding:
Example 1: If a company's sales increased from $50,000 to $60,000, what is the percentage increase?
- Solution: The increase is $10,000 ($60,000 - $50,000). The percentage increase is calculated as ($10,000 / $50,000) x 100% = 20%.
Example 2: A dress is on sale for $45 after a 20% discount. What was the original price?
- Solution: Let 'x' be the original price. After a 20% discount, the price is 80% of the original price (100% - 20% = 80%). Therefore, 0.8x = $45. Solving for x: x = $45 / 0.8 = $56.25.
Example 3: If you invest $1000 at a 5% annual interest rate compounded annually, how much will you have after 2 years?
- Solution: Year 1: $1000 x 1.05 = $1050. Year 2: $1050 x 1.05 = $1102.50.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems, as demonstrated through the question "12 is what percent of 60?", is a valuable skill with applications across numerous areas. Understanding the different methods—the formula method, the proportion method, and calculator usage—enables flexibility and efficiency in tackling various percentage calculations. By mastering these techniques and understanding the underlying principles, you'll be well-equipped to confidently handle percentage problems in your academic, professional, and personal life. Remember that consistent practice is key to solidifying your understanding and improving your problem-solving skills. Don't hesitate to tackle more challenging problems to further enhance your mastery of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Is Baking Soda An Element Or A Compound
Apr 01, 2025
-
33 Out Of 50 As A Percentage
Apr 01, 2025
-
How Much Is 58 Kilos In Pounds
Apr 01, 2025
-
22 5 Out Of 30 As A Percentage
Apr 01, 2025
-
How Do You Write 2 As A Decimal
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
