12 Out Of 18 As A Percent
Kalali
Apr 13, 2025 · 5 min read
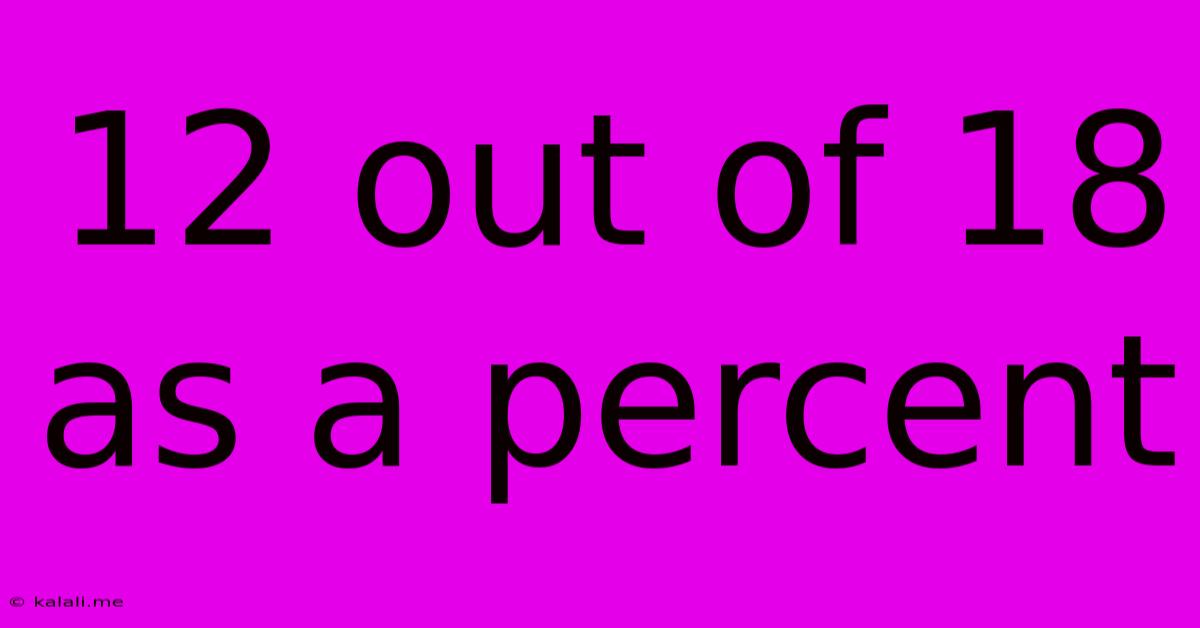
Table of Contents
12 out of 18 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. This article dives deep into calculating percentages, using the example of "12 out of 18" as a springboard to explore various methods and related concepts. We'll cover the basic calculation, different approaches, real-world applications, and even delve into advanced percentage problems to solidify your understanding. By the end, you'll be confident in tackling any percentage calculation you encounter.
What is a Percentage?
A percentage represents a fraction of 100. It expresses a proportion or rate relative to a whole. The term "percent" literally means "out of one hundred" – "per cent" being Latin for "out of one hundred". Therefore, 50% means 50 out of 100, which simplifies to one-half (1/2) or 0.5 as a decimal.
Calculating 12 out of 18 as a Percentage:
The core concept is simple: to find the percentage, divide the part (12) by the whole (18), then multiply the result by 100.
-
Step 1: Divide the part by the whole: 12 / 18 = 0.666... (This is a recurring decimal)
-
Step 2: Multiply by 100: 0.666... x 100 = 66.666...%
-
Step 3: Round to desired precision: Depending on the context, you might round the result. Commonly, you would round to two decimal places: 66.67%.
Therefore, 12 out of 18 is 66.67%.
Alternative Methods for Percentage Calculation:
While the above method is the most straightforward, several alternative approaches can be equally effective, especially for mental calculations or when dealing with simpler fractions:
-
Simplifying Fractions: Before converting to a percentage, simplify the fraction 12/18. Both numbers are divisible by 6, resulting in 2/3. Knowing that 1/3 is approximately 33.33%, 2/3 is approximately 66.67%. This method is particularly helpful when dealing with easily simplifiable fractions.
-
Using Proportions: Set up a proportion: 12/18 = x/100. Cross-multiply to solve for x: 18x = 1200. Divide both sides by 18: x = 66.67%. This method is useful for understanding the underlying relationship between fractions and percentages.
-
Using a Calculator: Modern calculators have a percentage function that simplifies the process significantly. Simply enter 12 ÷ 18 × 100, and the calculator will directly display the percentage. This is the most efficient method for complex or less intuitive numbers.
Real-World Applications of Percentage Calculations:
Percentage calculations are ubiquitous in daily life and professional settings. Here are a few examples:
-
Calculating Grades: If you scored 12 out of 18 on a test, your percentage score is 66.67%.
-
Discount Calculations: A 20% discount on a $100 item means a reduction of $20 (20% of $100). The final price would be $80.
-
Tax Calculations: A 5% sales tax on a $50 purchase would be $2.50 (5% of $50). The total cost would be $52.50.
-
Financial Analysis: Percentage changes in stock prices, interest rates, and investment returns are essential for understanding financial performance. A 10% increase in a $1,000 investment would result in a $100 gain.
-
Statistics and Data Analysis: Percentages are widely used to represent proportions in data sets, making it easier to visualize and interpret trends and patterns.
Understanding Percentage Increase and Decrease:
Calculating percentage increase or decrease involves comparing two values. The formula is:
[(New Value - Old Value) / Old Value] x 100
For example, if your salary increased from $50,000 to $60,000, the percentage increase is:
[($60,000 - $50,000) / $50,000] x 100 = 20%
Advanced Percentage Problems:
Let's explore some more complex scenarios that build upon the fundamental concepts:
-
Finding the Original Value: If a discounted price of an item is $80 after a 20% discount, what was the original price? Let 'x' be the original price. Then, 0.8x = $80. Solving for x, we find x = $100.
-
Multiple Percentage Changes: If a price increases by 10% and then decreases by 10%, the final price is not the same as the original price. This is because the second percentage change is calculated on the new value, not the original value. For instance, a $100 item increased by 10% becomes $110. A 10% decrease on $110 results in $99.
-
Compound Interest: Compound interest calculates interest on both the principal amount and accumulated interest. Understanding compound interest is crucial for long-term investments and loan calculations. The formula for compound interest is A = P (1 + r/n)^(nt), where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Tips for Mastering Percentage Calculations:
-
Practice Regularly: The key to mastering percentages is consistent practice. Work through various examples and gradually increase the complexity of the problems.
-
Use Visual Aids: Diagrams and charts can help visualize percentage relationships, especially when comparing multiple values.
-
Understand the Underlying Concepts: Don't just memorize formulas; understand the logic behind them. This will make it easier to adapt to different situations and solve unfamiliar problems.
-
Utilize Online Resources: Numerous websites and apps offer practice problems and tutorials on percentage calculations.
-
Break Down Complex Problems: If you encounter a complex problem, break it down into smaller, manageable steps. This will make the overall calculation less daunting.
Conclusion:
Calculating percentages, even seemingly simple ones like "12 out of 18," is a fundamental skill with broad applications. This article has provided a comprehensive overview of calculating percentages, including alternative methods, real-world examples, and advanced concepts. By understanding the underlying principles and practicing regularly, you can confidently tackle any percentage-related challenge. Remember to choose the method best suited to the context and always check your work to ensure accuracy. Mastering percentages empowers you to navigate the numerical world with greater confidence and precision.
Latest Posts
Latest Posts
-
How Much Is 48 Oz Of Water
Jul 18, 2025
-
How Long Does It Take To Drive 2000 Miles
Jul 18, 2025
-
How Many Grams In A Teaspoon Of Cinnamon
Jul 18, 2025
-
How Long To Heat Water In Microwave
Jul 18, 2025
-
40 Oz Of Water Is How Many Cups
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 18 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.