13 Out Of 20 As A Percentage
Kalali
Mar 09, 2025 · 4 min read
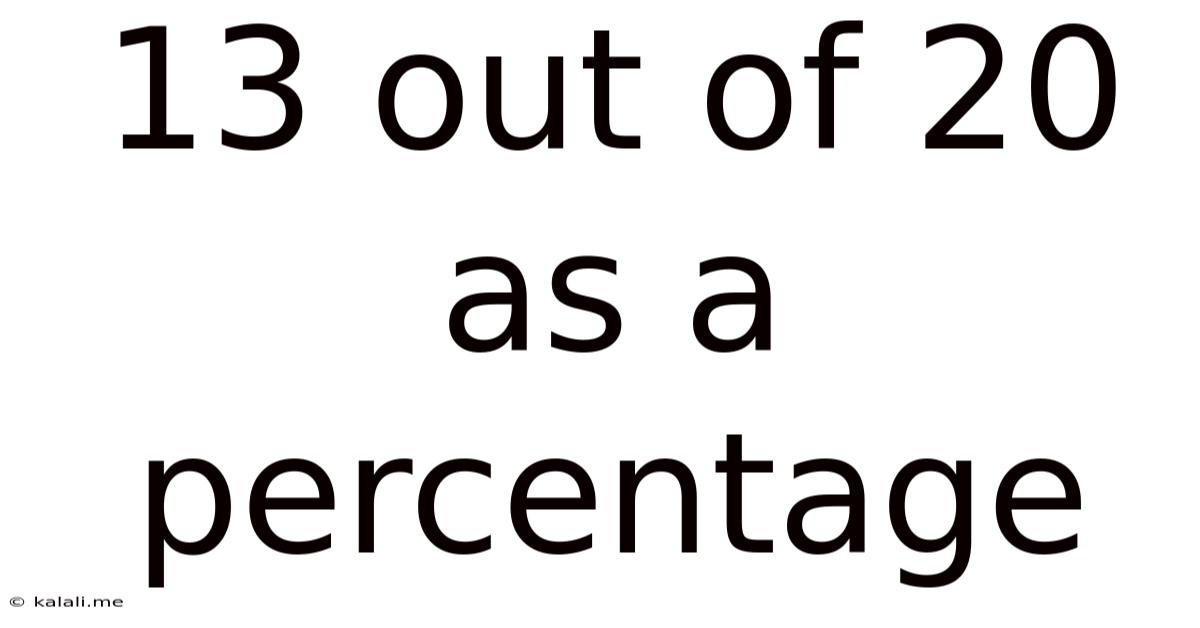
Table of Contents
13 Out of 20 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis and everyday life situations. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating effectively. This article delves deep into the calculation of 13 out of 20 as a percentage, exploring various methods and highlighting its practical applications. We will also explore related percentage calculations and offer strategies for tackling similar problems.
Understanding Fractions and Percentages
Before diving into the specific calculation, let's solidify our understanding of fractions and percentages. A fraction represents a part of a whole. For instance, 13/20 signifies 13 parts out of a total of 20 parts. A percentage, denoted by the symbol %, expresses a fraction as a portion of 100. Therefore, converting a fraction to a percentage involves determining what portion of 100 the fraction represents.
Calculating 13 Out of 20 as a Percentage: The Step-by-Step Guide
There are several ways to calculate 13 out of 20 as a percentage. Let's explore the most common methods:
Method 1: Using the Basic Formula
The fundamental formula for converting a fraction to a percentage is:
(Part / Whole) * 100%
In our case:
- Part: 13
- Whole: 20
Substituting these values into the formula:
(13 / 20) * 100% = 65%
Therefore, 13 out of 20 is equal to 65%.
Method 2: Converting the Fraction to a Decimal
This method involves first converting the fraction to a decimal and then multiplying by 100%.
- Convert the fraction to a decimal: 13 / 20 = 0.65
- Multiply the decimal by 100%: 0.65 * 100% = 65%
This method yields the same result: 65%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We can set up a proportion:
13/20 = x/100
To solve for x (the percentage), cross-multiply:
20x = 1300
x = 1300 / 20
x = 65
Therefore, 13 out of 20 is 65%.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in various real-world scenarios:
1. Academic Performance:
Imagine a student scoring 13 out of 20 on a quiz. Understanding that this equates to 65% allows for easy comparison with other assessments and helps gauge overall academic performance.
2. Sales and Discounts:
Retailers frequently offer discounts expressed as percentages. Knowing how to calculate percentages helps consumers determine the actual price reduction and make informed purchasing decisions. For example, a 65% discount on a $100 item would result in a $65 reduction, bringing the final price down to $35.
3. Financial Analysis:
In finance, percentages are used extensively to analyze financial statements, calculate interest rates, and track investment performance. For instance, if an investment grows from $100 to $165, the percentage increase is 65%.
4. Data Interpretation:
Analyzing survey results, statistical data, and scientific research frequently requires calculating percentages to understand trends, make predictions, and draw meaningful conclusions. For example, if a survey reveals that 13 out of 20 respondents prefer a particular product, this translates to 65% preference.
5. Everyday Life:
From calculating tips in restaurants to determining the percentage of ingredients in a recipe, percentage calculations are frequently used in our everyday lives.
Related Percentage Calculations and Problem-Solving Strategies
Mastering the calculation of 13 out of 20 as a percentage lays a solid foundation for tackling other percentage-related problems. Let's explore some related calculations and strategies:
1. Calculating the Percentage of a Larger Number:
What if you need to find 65% of a larger number, say 500? The formula is:
(Percentage/100) * Number = Result
(65/100) * 500 = 325
Therefore, 65% of 500 is 325.
2. Finding the Whole Number When Given a Percentage and Part:
If you know that 65% of a number is 195, how do you find the original number? You can set up a proportion:
65/100 = 195/x
Cross-multiply and solve for x:
65x = 19500
x = 300
Therefore, the original number is 300.
3. Calculating Percentage Increase or Decrease:
To calculate the percentage increase or decrease, use the following formula:
[(New Value - Old Value) / Old Value] * 100%
For example, if a value increases from 200 to 330, the percentage increase is:
[(330 - 200) / 200] * 100% = 65%
Conclusion: Mastering Percentages for Success
Calculating percentages is a versatile skill with wide-ranging applications. Understanding the various methods for converting fractions to percentages, like the ones demonstrated with the example of 13 out of 20, empowers you to effectively interpret data, make informed decisions, and solve problems across diverse fields. By mastering these techniques and employing the problem-solving strategies outlined in this article, you’ll be well-equipped to navigate the world of percentages with confidence and competence. Remember to practice regularly to solidify your understanding and build proficiency in this essential skill. The ability to effortlessly calculate and interpret percentages is a key asset in both academic and professional contexts, contributing significantly to success in various endeavors.
Latest Posts
Latest Posts
-
How Do You Say Pickles In Spanish
Jul 06, 2025
-
How Much Is 1000 Hours In Days
Jul 06, 2025
-
Sic A Parrot On The Guild Emissary
Jul 06, 2025
-
How Many Slices Of Turkey Is 3 Oz
Jul 06, 2025
-
Which Word Best Describes The Tone Of The Passage
Jul 06, 2025
Related Post
Thank you for visiting our website which covers about 13 Out Of 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.