14 Out Of 21 As A Percentage
Kalali
Apr 24, 2025 · 5 min read
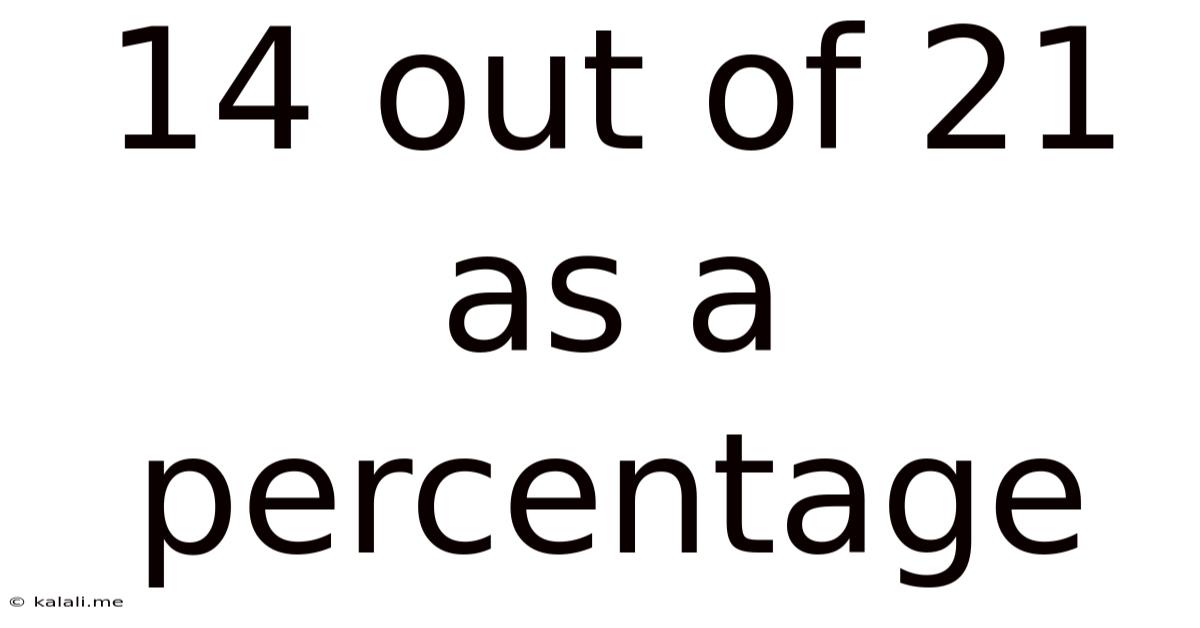
Table of Contents
14 Out of 21 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from finance and statistics to everyday life. Understanding how to express fractions as percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This article delves into the specific calculation of 14 out of 21 as a percentage, providing a step-by-step guide, exploring different methods, and offering broader context on percentage calculations. This comprehensive guide will equip you with the knowledge to confidently tackle similar percentage problems in the future. We will also examine real-world applications and explore common mistakes to avoid.
What is a Percentage?
Before diving into the calculation, let's establish a clear understanding of what a percentage represents. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, which simplifies to one-half (1/2) or 0.5 in decimal form. Percentages are used to express proportions, rates, and changes in various contexts.
Calculating 14 out of 21 as a Percentage: The Standard Method
The most straightforward method to calculate 14 out of 21 as a percentage involves three simple steps:
-
Express the ratio as a fraction: The phrase "14 out of 21" translates directly to the fraction 14/21.
-
Convert the fraction to a decimal: Divide the numerator (14) by the denominator (21): 14 ÷ 21 = 0.666666... (This is a recurring decimal).
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.666666... × 100 = 66.67% (rounded to two decimal places).
Therefore, 14 out of 21 is equal to 66.67%.
Alternative Calculation Methods
While the standard method is perfectly adequate, alternative methods can offer a different perspective and might be more efficient depending on the specific scenario.
-
Simplifying the Fraction: Before converting to a decimal, simplifying the fraction can make the calculation easier. Both 14 and 21 are divisible by 7: 14/21 simplifies to 2/3. Converting 2/3 to a decimal (2 ÷ 3 = 0.666666...) and then to a percentage (0.666666... × 100 = 66.67%) yields the same result.
-
Using Proportions: You can set up a proportion to solve for the percentage:
14/21 = x/100
Cross-multiply: 21x = 1400
Solve for x: x = 1400/21 = 66.67%
Understanding the Significance of Rounding
In the calculations above, we rounded the decimal 0.666666... to 0.67. The number of decimal places you round to depends on the level of precision required. In many contexts, two decimal places are sufficient, offering a balance between accuracy and simplicity. However, for highly precise applications, more decimal places might be necessary. For instance, in financial calculations, rounding errors can accumulate and significantly impact the final results. Always consider the context of your calculation when determining the appropriate level of rounding.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world situations:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns. For example, if a store offers a 20% discount on an item, you'd use percentage calculations to determine the final price.
-
Statistics: Analyzing data sets, interpreting survey results, understanding population demographics, and expressing probabilities. For instance, if 14 out of 21 people surveyed prefer a particular brand, the percentage calculation helps represent this preference in a concise and easily understood manner.
-
Science: Expressing concentrations, efficiencies, and experimental results. In chemistry, for instance, percentage composition is frequently used to represent the relative amounts of different elements in a compound.
-
Education: Calculating grades, assessing student performance, and tracking progress.
-
Everyday Life: Calculating tips, understanding sales, determining proportions in recipes, and managing budgets.
Common Mistakes to Avoid When Calculating Percentages
Several common errors can lead to inaccurate results. Being mindful of these pitfalls can ensure accuracy and avoid misinterpretations.
-
Incorrect order of operations: When working with multiple operations, always follow the order of operations (PEMDAS/BODMAS).
-
Mistakes in decimal-to-percentage conversion: Remember to multiply by 100 when converting a decimal to a percentage. Forgetting this step is a frequent error.
-
Rounding errors: While rounding is often necessary, excessive or premature rounding can accumulate errors, especially in complex calculations.
-
Misunderstanding the context: Ensure that you correctly interpret the question and identify the relevant quantities. For instance, understanding whether "14 out of 21" refers to a part of a whole or a change over time is crucial.
Expanding on Percentage Concepts: Related Calculations
Beyond calculating a simple percentage like 14 out of 21, understanding related concepts strengthens your grasp of percentages.
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. For example, if a value increases from 20 to 25, the percentage increase is calculated as: [(25-20)/20] x 100 = 25%.
-
Percentage Points: This represents the absolute difference between two percentages. For instance, if the unemployment rate rises from 5% to 8%, the increase is 3 percentage points, not 60% (which would be the percentage increase).
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages accurately and efficiently is a valuable skill. By understanding the fundamental principles, different calculation methods, and common pitfalls, you can confidently tackle various percentage problems. This article provided a detailed explanation of calculating 14 out of 21 as a percentage (66.67%), along with broader context on percentage calculations and real-world applications. Remember to practice regularly and always double-check your work to ensure accuracy. Mastering percentages empowers you to analyze data, make informed decisions, and communicate numerical information effectively across numerous disciplines. From simple everyday tasks to complex financial analyses, a strong understanding of percentages is a valuable asset.
Latest Posts
Latest Posts
-
How Long Is 100cm In Inches
Apr 25, 2025
-
23 Out Of 30 Is What Percent
Apr 25, 2025
-
What Is 55 As A Fraction
Apr 25, 2025
-
What Percent Is 8 Out Of 30
Apr 25, 2025
-
What Is 35 Percent Of 20
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about 14 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.