15 2 As A Mixed Number
Kalali
Apr 17, 2025 · 6 min read
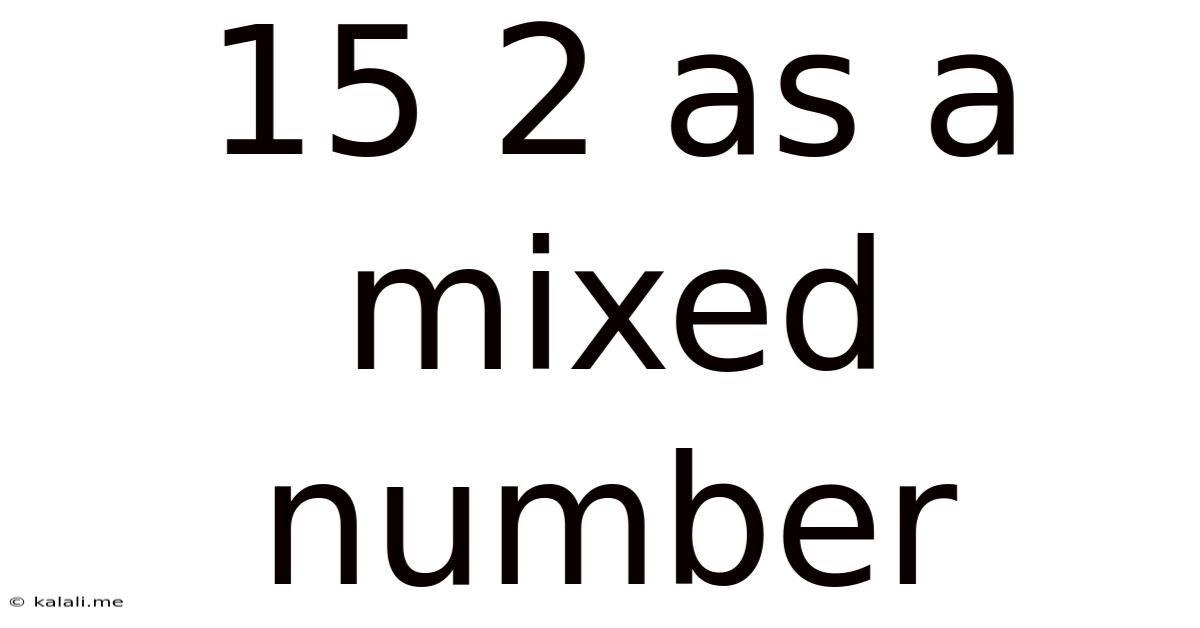
Table of Contents
15/2 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve deep into converting the improper fraction 15/2 into a mixed number, explaining the process step-by-step and exploring related concepts. We'll also touch upon the practical applications of this conversion and offer some helpful tips for mastering fraction manipulation. This guide aims to provide a thorough understanding, going beyond a simple answer and providing the context needed for true comprehension.
Meta Description: Learn how to convert the improper fraction 15/2 into a mixed number. This detailed guide explains the process, explores related concepts, and offers practical applications for mastering fraction manipulation.
What is a Mixed Number?
Before diving into the conversion, let's clarify what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ½, 3 ⅓, and 7 ⅘ are all mixed numbers. They represent a quantity larger than one whole unit.
What is an Improper Fraction?
Conversely, an improper fraction is a fraction where the numerator is greater than or equal to the denominator. Our focus, 15/2, is an improper fraction because 15 (the numerator) is larger than 2 (the denominator). Improper fractions represent a quantity equal to or greater than one whole unit. They are often less intuitive to understand than mixed numbers in representing quantities.
Converting 15/2 to a Mixed Number: The Step-by-Step Process
The conversion of 15/2 to a mixed number involves a simple division process:
-
Divide the numerator by the denominator: Divide 15 by 2. This gives us a quotient of 7 and a remainder of 1.
-
The quotient becomes the whole number part: The quotient, 7, becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction part: The remainder, 1, becomes the numerator of the fraction part.
-
The denominator remains the same: The denominator of the fraction part remains the same as the original denominator, which is 2.
Therefore, 15/2 as a mixed number is 7 1/2.
Visualizing the Conversion
Imagine you have 15 identical items, and you want to group them into pairs (groups of 2). You can form 7 complete pairs with 1 item remaining. This visually represents the 7 whole groups (the whole number 7) and the single remaining item (the fraction 1/2).
Why Convert Improper Fractions to Mixed Numbers?
Converting improper fractions to mixed numbers often makes it easier to:
-
Understand the quantity: Mixed numbers provide a more intuitive representation of a quantity larger than one. It's easier to grasp the concept of "7 and a half" than "15 halves."
-
Perform calculations: Some mathematical operations, like addition and subtraction, are simpler with mixed numbers, especially when dealing with mixed numbers and whole numbers together.
-
Solve real-world problems: In practical applications like measuring lengths, dividing resources, or cooking, mixed numbers are often preferred for their clarity and ease of understanding.
-
Compare fractions: Comparing mixed numbers is sometimes easier than comparing improper fractions, especially when visually estimating the size of fractions.
-
Improve mathematical fluency: Practicing this conversion solidifies your understanding of fractions and division.
Practice Problems: Converting Improper Fractions to Mixed Numbers
Let's practice converting a few more improper fractions to mixed numbers to solidify your understanding:
-
22/5: Divide 22 by 5. The quotient is 4, and the remainder is 2. Therefore, 22/5 = 4 2/5.
-
17/3: Divide 17 by 3. The quotient is 5, and the remainder is 2. Therefore, 17/3 = 5 2/3.
-
25/4: Divide 25 by 4. The quotient is 6, and the remainder is 1. Therefore, 25/4 = 6 1/4.
-
31/6: Divide 31 by 6. The quotient is 5, and the remainder is 1. Therefore, 31/6 = 5 1/6.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting mixed numbers back into improper fractions. This is often necessary when performing multiplication or division with fractions. The process is as follows:
-
Multiply the whole number by the denominator: Multiply the whole number by the denominator of the fraction.
-
Add the numerator: Add the result to the numerator of the fraction.
-
Keep the denominator the same: The denominator remains unchanged.
Let's convert our example, 7 1/2, back to an improper fraction:
-
7 (whole number) * 2 (denominator) = 14
-
14 + 1 (numerator) = 15
-
The denominator remains 2.
Therefore, 7 1/2 = 15/2.
Applications of Fractions and Mixed Numbers in Real Life
Fractions and mixed numbers are ubiquitous in everyday life. Here are some examples:
-
Cooking and Baking: Recipes often use fractions and mixed numbers for ingredient measurements (e.g., 2 ½ cups of flour).
-
Construction and Engineering: Precise measurements in construction and engineering rely heavily on fractions and their decimal equivalents.
-
Finance: Calculating interest, discounts, and shares often involves fractions and percentages (which are essentially fractions with a denominator of 100).
-
Time Measurement: Time is often expressed using fractions (e.g., ¼ hour, ½ hour).
-
Data Analysis: Representing proportions and ratios frequently utilizes fractions.
Advanced Concepts Related to Fractions
Understanding the conversion of 15/2 to a mixed number lays the foundation for more advanced concepts in mathematics, including:
-
Decimal Representation: Improper fractions and mixed numbers can be converted to decimal numbers through division. For example, 15/2 = 7.5.
-
Fraction Operations: Mastering fraction addition, subtraction, multiplication, and division becomes significantly easier once you understand the relationship between improper fractions and mixed numbers.
-
Algebra: Fractions and mixed numbers are frequently used in algebraic equations and problem-solving.
-
Calculus: Advanced mathematical concepts such as limits and derivatives often involve working with fractions and their properties.
Tips for Mastering Fraction Manipulation
-
Practice regularly: Consistent practice is key to mastering fraction manipulation. Work through various problems and challenge yourself with different types of fractions.
-
Visual aids: Use visual aids like diagrams and manipulatives to help you understand the concepts.
-
Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or online resources if you're struggling with a particular concept.
-
Break down complex problems: If you're facing a complex problem involving fractions, break it down into smaller, more manageable steps.
-
Use online resources: Many excellent online resources, including interactive exercises and tutorials, can help you improve your understanding of fractions.
Conclusion: More Than Just a Simple Conversion
Converting 15/2 to the mixed number 7 1/2 is more than a simple mathematical operation. It represents a fundamental understanding of fractions, their representation, and their practical applications. Mastering this conversion builds a solid foundation for more complex mathematical concepts and problem-solving skills. By understanding the underlying principles and practicing regularly, you can confidently navigate the world of fractions and their numerous applications in various fields. Remember, the key to mastery lies in consistent practice and a deep understanding of the underlying concepts.
Latest Posts
Latest Posts
-
35 8 As A Mixed Number
Apr 19, 2025
-
What Is The Domain Of The Function Graphed Below
Apr 19, 2025
-
What Is 6 Ft 1 In Cm
Apr 19, 2025
-
How Much Is 24 Celsius In Fahrenheit
Apr 19, 2025
-
How Many Feet Is 36 Meters
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 15 2 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.