15 51 26 62 37 73 48
Kalali
Jul 19, 2025 · 5 min read
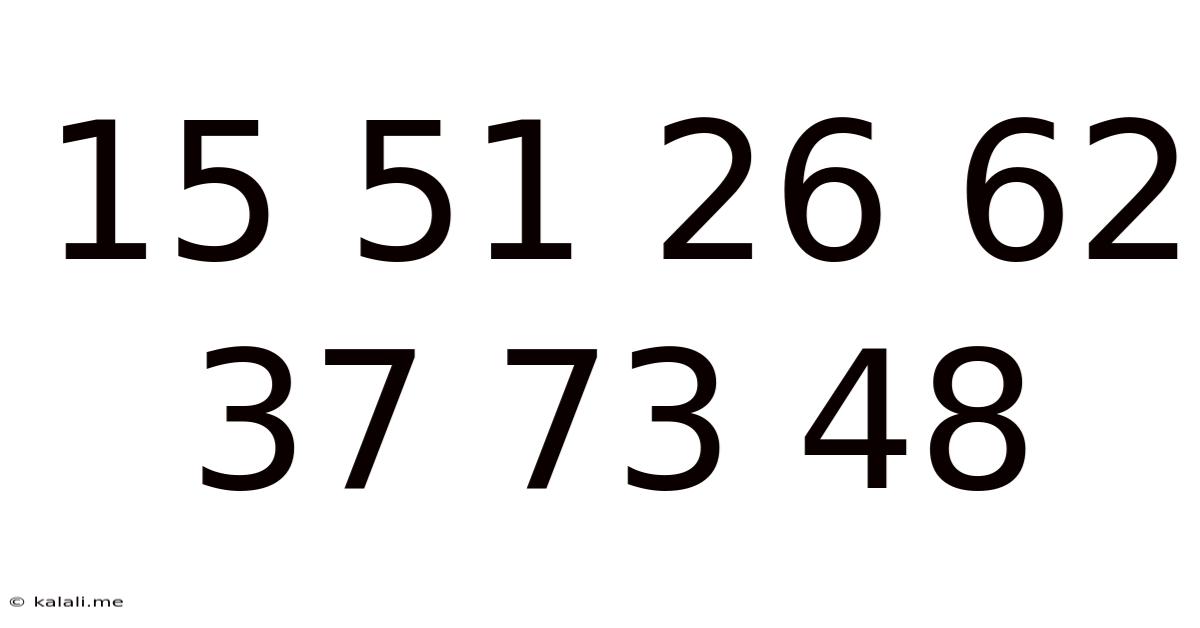
Table of Contents
Decoding the Sequence: Exploring the Patterns and Possibilities Within 15 51 26 62 37 73 48
This seemingly random sequence of numbers – 15, 51, 26, 62, 37, 73, 48 – presents a fascinating challenge. At first glance, it appears arbitrary. However, a closer examination reveals potential underlying patterns and relationships, inviting us to explore the world of number sequences, mathematical logic, and the very nature of pattern recognition. This article delves deep into the sequence, exploring various approaches to understanding its structure and speculating on possible generating rules. We'll consider potential mathematical operations, statistical analyses, and even the possibility of hidden codes or cryptographic elements. The goal isn't necessarily to find the definitive answer, as multiple interpretations are possible, but rather to illustrate the analytical processes involved in deciphering numerical sequences and the creative problem-solving inherent in such an endeavor.
Understanding Numerical Sequences and Pattern Recognition:
Before diving into the specifics of the sequence 15, 51, 26, 62, 37, 73, 48, it's crucial to understand the fundamental concepts underlying numerical sequences and the importance of pattern recognition. Numerical sequences are ordered lists of numbers, often following a specific rule or pattern. These patterns can be simple, like arithmetic progressions (constant difference between consecutive terms) or geometric progressions (constant ratio between consecutive terms), or they can be significantly more complex, involving combinations of operations, recursive relationships, or even chaotic behavior.
Pattern recognition is a critical cognitive skill, crucial in various fields, from mathematics and computer science to data analysis and cryptography. It involves identifying regularities, similarities, and relationships within seemingly random data. In the context of numerical sequences, pattern recognition allows us to formulate hypotheses about the underlying rules governing the sequence's generation. This often involves trial and error, testing various mathematical operations and looking for consistent results.
Analyzing the Sequence: Initial Observations and Potential Patterns:
Let's begin by examining the sequence 15, 51, 26, 62, 37, 73, 48 for readily apparent patterns.
-
Differences between consecutive terms: Calculating the differences between consecutive terms reveals no immediately obvious pattern: 36, -25, 36, -25, 36, -25. This suggests a potential alternating pattern involving a difference of 36 followed by a difference of -25. This is a promising lead.
-
Alternating subsequences: We can separate the sequence into two subsequences: 15, 26, 37, 48 and 51, 62, 73. Each of these subsequences shows a consistent difference of 11. This is a strong indication of a structured pattern.
-
Sum of digits: Let's look at the sum of the digits for each number: 6, 6, 8, 8, 10, 10, 12. This shows an alternating pattern where the sum of digits increases by 2 each time. While not directly revealing the generation rule, it's a noteworthy observation hinting at a possible underlying structure.
-
Modular Arithmetic: Examining the remainders when the numbers are divided by various integers might reveal hidden patterns. For instance, considering modulo 11 reveals interesting relationships.
Formulating Hypotheses and Testing Potential Rules:
Based on our initial observations, several hypotheses can be formulated about the sequence's generation:
Hypothesis 1: Alternating Arithmetic Progression: The sequence could be generated by alternating between two arithmetic progressions: one with a common difference of 11, starting at 15, and another with a common difference of 11, starting at 51. This directly explains the alternating subsequences observed earlier.
Hypothesis 2: A Recursive Relationship: A more complex hypothesis could involve a recursive relationship where each term is a function of the previous terms. This would require more sophisticated mathematical analysis to determine the precise function.
Hypothesis 3: A Combination of Operations: It's possible the sequence is generated by applying a combination of arithmetic and potentially other mathematical operations. For example, adding a specific number to one term and subtracting another number from the next.
Testing the Hypotheses:
Let's test Hypothesis 1:
- Sequence 1: 15, 26, 37, 48 (common difference: 11)
- Sequence 2: 51, 62, 73 (common difference: 11)
This hypothesis aligns perfectly with our initial observations, suggesting a relatively simple generation rule. However, further investigation is needed to determine if other hypotheses might also fit the sequence.
Expanding the Sequence and Predicting Future Terms:
If Hypothesis 1 is correct, we can confidently predict future terms in the sequence: the next term in the first subsequence would be 59, followed by 84 in the second subsequence, then 70, and so on. This predictive capability is a key test of the validity of our hypothesis. The ability to accurately predict future terms strongly supports the hypothesis.
Beyond the Numbers: Considering Broader Applications
The analysis of this seemingly simple numerical sequence illustrates broader principles applicable to diverse fields:
-
Cryptography: Numerical sequences are frequently used in cryptography to generate keys and encrypt data. Understanding the patterns and structures within sequences is crucial in cryptanalysis, the process of breaking codes.
-
Data Analysis: In data analysis, identifying patterns in numerical data is essential for drawing meaningful conclusions and making informed decisions. Techniques similar to those used here are applied to analyze large datasets in various fields, including finance, science, and engineering.
-
Computer Science: Algorithms for generating and analyzing numerical sequences are fundamental in computer science. These algorithms have applications in areas like sorting, searching, and data compression.
-
Mathematics: Number theory, a branch of mathematics, is deeply concerned with the properties and relationships between numbers. Analyzing numerical sequences helps uncover fundamental mathematical concepts and relationships.
Conclusion: The Power of Pattern Recognition and Analytical Thinking
The seemingly random sequence 15, 51, 26, 62, 37, 73, 48, despite its initial appearance, exhibits underlying structure and patterns. Through careful observation, systematic analysis, and the formulation and testing of hypotheses, we've been able to identify a likely generation rule. While other explanations might exist, the process of uncovering these patterns demonstrates the power of analytical thinking and pattern recognition. The ability to identify and understand patterns is crucial across various disciplines, providing insights that can lead to new discoveries and innovations. This exploration highlights the importance of methodical investigation and the rewards of persistent inquiry in unraveling the mysteries hidden within seemingly random data. Further investigation, exploring more complex mathematical functions and statistical analyses, could potentially uncover additional layers of complexity or alternative interpretations of the sequence. The pursuit of knowledge is a continuous process, and even a simple numerical sequence can offer a rich and rewarding journey of exploration.
Latest Posts
Latest Posts
-
Large Size Crystals Are Know As Phaneritic Are Called
Jul 19, 2025
-
What Time Is A Quarter To 3
Jul 19, 2025
-
8am To 12pm Is How Many Hours
Jul 19, 2025
-
Which Part Of An Optical Microscope Contains A Magnifying Lens
Jul 19, 2025
-
Does Dog Dewormer Need To Be Refrigerated
Jul 19, 2025
Related Post
Thank you for visiting our website which covers about 15 51 26 62 37 73 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.