15 8 As A Mixed Number
Kalali
Apr 15, 2025 · 5 min read
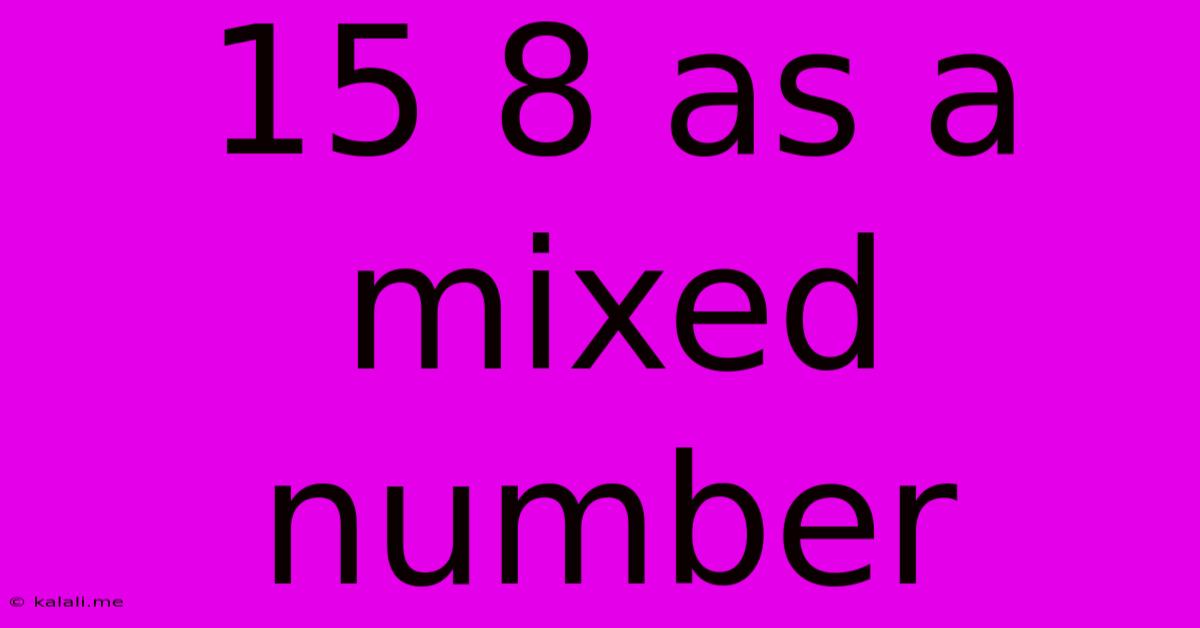
Table of Contents
Understanding 15/8 as a Mixed Number: A Comprehensive Guide
Meta Description: Learn how to convert the improper fraction 15/8 into a mixed number. This comprehensive guide explains the process step-by-step, including helpful examples and tips for mastering fraction conversion. We'll also explore related concepts and applications.
Converting fractions is a fundamental skill in mathematics, essential for various applications from basic arithmetic to advanced calculus. One common type of fraction conversion involves transforming an improper fraction (where the numerator is larger than the denominator) into a mixed number (a combination of a whole number and a proper fraction). This guide focuses on understanding and mastering the conversion of the improper fraction 15/8 into its equivalent mixed number form. We'll explore the process in detail, delve into the underlying concepts, and provide practical examples to reinforce your learning.
What is a Mixed Number?
A mixed number is a way of representing a fraction that is greater than one. It combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ½, 3 ¼, and 2 ⅔ are all mixed numbers. These numbers represent a quantity that's more than a whole unit. Understanding mixed numbers is crucial in many real-world scenarios, from measuring ingredients in cooking to calculating distances and areas.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 7/4, 15/8, and 9/9 are all improper fractions. These fractions represent a quantity that is equal to or greater than one whole unit. While perfectly valid mathematically, improper fractions are often less intuitive to understand compared to mixed numbers in everyday contexts.
Converting 15/8 to a Mixed Number: A Step-by-Step Guide
The process of converting an improper fraction like 15/8 into a mixed number involves division. Here's a step-by-step guide:
Step 1: Divide the Numerator by the Denominator
Divide the numerator (15) by the denominator (8).
15 ÷ 8 = 1 with a remainder of 7
Step 2: Identify the Whole Number
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
Step 3: Identify the Remainder
The remainder from the division becomes the numerator of the fractional part of the mixed number. The remainder here is 7.
Step 4: Keep the Original Denominator
The denominator of the fractional part remains the same as the denominator of the original improper fraction. The denominator stays as 8.
Step 5: Combine the Whole Number and the Fraction
Combine the whole number from Step 2 and the fraction from Steps 3 and 4 to form the mixed number.
Therefore, 15/8 as a mixed number is 1 ⁷⁄₈.
Visualizing the Conversion
Imagine you have 15 slices of pizza, and each pizza has 8 slices. You can make one complete pizza (8 slices) and you'll have 7 slices left over. This represents 1 whole pizza and ⁷⁄₈ of another pizza, perfectly illustrating the mixed number 1 ⁷⁄₈.
Practical Applications of Mixed Numbers
Mixed numbers find widespread use in various real-world applications:
- Cooking and Baking: Recipes often use mixed numbers for ingredient measurements, such as 1 ½ cups of flour or 2 ⅔ teaspoons of baking powder.
- Measurement: Measuring lengths, weights, and volumes frequently involves mixed numbers, for example, 3 ¼ inches or 1 ⅝ pounds.
- Construction and Engineering: Precise measurements in construction and engineering often necessitate the use of mixed numbers for accuracy and clarity.
- Time: Representing durations often utilizes mixed numbers, such as 1 ½ hours or 2 ¾ minutes.
- Data Analysis: Mixed numbers can appear in statistical data and charts, requiring understanding for proper interpretation.
More Examples of Improper Fraction to Mixed Number Conversions
Let's look at a few more examples to solidify your understanding:
- 17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 ²/₅.
- 23/6: 23 ÷ 6 = 3 with a remainder of 5. Therefore, 23/6 = 3 ⁵⁄₆.
- 11/3: 11 ÷ 3 = 3 with a remainder of 2. Therefore, 11/3 = 3 ²/₃.
- 25/4: 25 ÷ 4 = 6 with a remainder of 1. Therefore, 25/4 = 6 ¼.
- 32/7: 32 ÷ 7 = 4 with a remainder of 4. Therefore, 32/7 = 4 ⁴⁄₇.
Converting Mixed Numbers Back to Improper Fractions
The reverse process is also important. To convert a mixed number back to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: For example, in 1 ⁷⁄₈, multiply 1 by 8, which equals 8.
- Add the numerator: Add the result from step 1 to the numerator of the fraction. 8 + 7 = 15
- Keep the denominator the same: The denominator remains 8.
- Combine to form the improper fraction: The resulting improper fraction is 15/8.
Tips for Mastering Fraction Conversion
- Practice regularly: Consistent practice is key to mastering fraction conversions. Work through numerous examples to build your confidence and understanding.
- Visual aids: Utilize visual aids like diagrams or fraction bars to help visualize the concept.
- Real-world applications: Connect fraction conversions to real-world situations to make learning more engaging and memorable.
- Check your work: Always double-check your calculations to ensure accuracy.
- Use online resources: Numerous online tools and calculators can assist you in verifying your answers and reinforcing your understanding.
Advanced Concepts Related to Fraction Conversion
While this guide focuses on basic fraction conversion, several advanced concepts build upon this foundation:
- Equivalent Fractions: Understanding equivalent fractions is crucial for simplifying fractions and performing various mathematical operations. Equivalent fractions represent the same value but have different numerators and denominators.
- Fraction Operations: Mastering fraction addition, subtraction, multiplication, and division forms the basis for more advanced mathematical applications.
- Decimals and Fractions: Converting between decimals and fractions expands the applications of fraction manipulation.
- Algebraic Fractions: Algebraic fractions involve variables and are a cornerstone of algebraic manipulation and problem-solving.
Conclusion: Mastering the Art of Fraction Conversion
Converting improper fractions to mixed numbers, as demonstrated with the example of 15/8, is a fundamental skill in mathematics with wide-ranging applications. By understanding the underlying principles and practicing regularly, you can confidently navigate fraction conversions and apply this knowledge to various real-world situations. Remember the steps, visualize the concept, and practice consistently to build your proficiency. With dedicated effort, mastering fraction conversion will significantly enhance your mathematical abilities.
Latest Posts
Latest Posts
-
What Episode Does Ichigo Get His Powers Back
Jul 05, 2025
-
Pokemon Mystery Dungeon Red Rescue Team Codes
Jul 05, 2025
-
How Much Is 25 20 Dollar Bills
Jul 05, 2025
-
How Many Apples In 3 Lb Bag
Jul 05, 2025
-
What Is Half A Quarter Of 400
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about 15 8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.