15 Is 30 Percent Of What Number
Kalali
Jul 22, 2025 · 4 min read
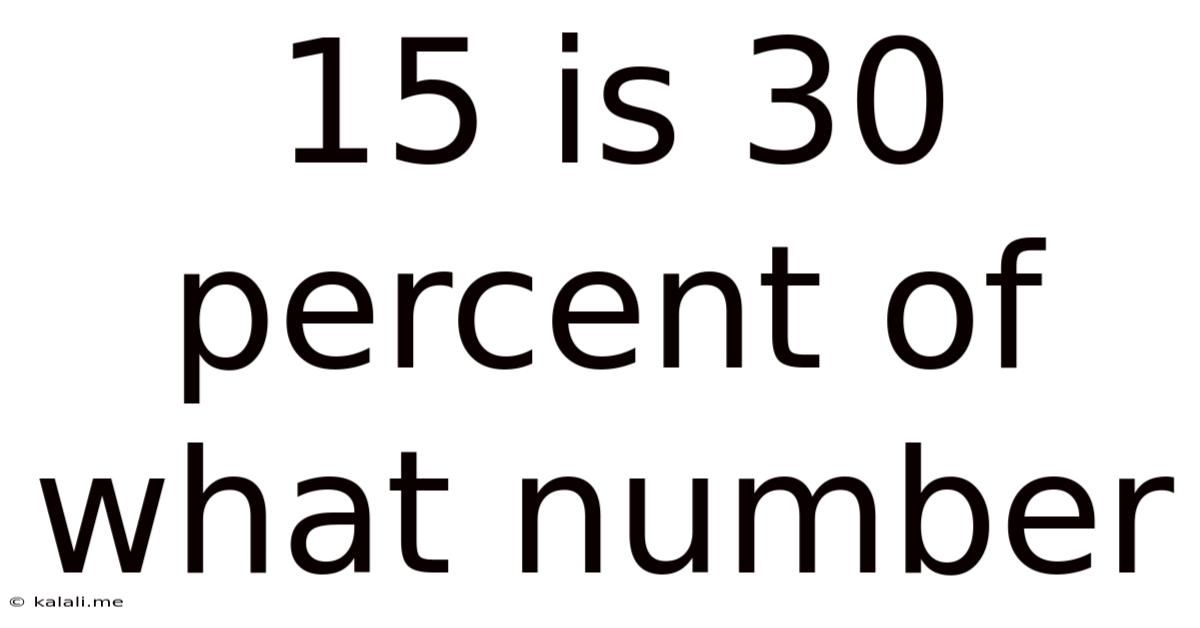
Table of Contents
15 is 30 Percent of What Number: A Comprehensive Guide to Percentage Calculations
This article will explore how to solve the problem "15 is 30 percent of what number?" We'll delve into the fundamental principles of percentages, providing multiple methods for solving this type of problem, and exploring practical applications in various fields. Understanding percentage calculations is crucial in numerous aspects of life, from everyday budgeting and shopping to more complex financial analysis and scientific applications. This guide aims to equip you with the knowledge and skills to confidently tackle similar percentage problems.
Understanding Percentages: The Foundation
Percentages represent fractions with a denominator of 100. The word "percent" literally means "out of one hundred." Therefore, 30% can be expressed as 30/100, or its decimal equivalent, 0.30. This fundamental understanding forms the basis for all percentage calculations.
Method 1: Using Proportions
This method is particularly helpful for visualizing the relationship between the parts and the whole. We can set up a proportion to solve for the unknown number:
- 15/x = 30/100
Where:
- 15 represents the part (30% of the unknown number).
- x represents the whole (the unknown number we're trying to find).
- 30/100 represents 30% as a fraction.
To solve this proportion, we can cross-multiply:
- 15 * 100 = 30 * x
- 1500 = 30x
Now, divide both sides by 30 to isolate x:
- x = 1500 / 30
- x = 50
Therefore, 15 is 30 percent of 50.
Method 2: Using the Decimal Equivalent
This method involves converting the percentage to its decimal equivalent and then setting up an equation. As mentioned earlier, 30% is equivalent to 0.30. We can express the problem as an equation:
- 0.30 * x = 15
To solve for x, divide both sides by 0.30:
- x = 15 / 0.30
- x = 50
Again, we find that 15 is 30 percent of 50.
Method 3: Using the Percentage Formula
The percentage formula provides a more direct approach:
- Percentage = (Part / Whole) * 100
We can rearrange this formula to solve for the "Whole" (the unknown number):
- Whole = (Part / Percentage) * 100
Substituting the values from our problem:
- Whole = (15 / 30) * 100
- Whole = 0.5 * 100
- Whole = 50
This confirms, once again, that 15 is 30 percent of 50.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, determining the final price of an item after a 20% discount requires calculating the percentage of the original price. Similarly, understanding compound interest necessitates proficiency in percentage calculations over time.
-
Business: Analyzing sales figures, market share, and cost-benefit analyses frequently involve percentage comparisons. Tracking key performance indicators (KPIs) within a business often involves expressing them as percentages for easy interpretation and comparison. Profitability analysis is another domain where an understanding of percentages is crucial.
-
Science: Many scientific disciplines use percentages to represent data, such as the concentration of a solution, the percentage of a specific element in a compound, or the error rate in an experiment. Experimental data often requires percentage-based representation for comparison purposes.
-
Everyday Life: Calculating tips in restaurants, understanding sales discounts, and interpreting survey results all rely on understanding percentages. Even something as simple as determining how much you saved by buying an item on sale involves a percentage calculation.
-
Data Analysis: Percentages are fundamental for summarizing and interpreting data. Presenting data in percentage form often enhances clarity and facilitates comparisons. Whether dealing with surveys, demographics, or market research, percentages are indispensable tools for understanding trends and patterns.
Advanced Percentage Problems & Techniques
While the problem "15 is 30 percent of what number?" is relatively straightforward, understanding the fundamental methods allows you to tackle more complex problems. This includes scenarios involving multiple percentages, successive percentages, and percentage increases or decreases. These more intricate problems often involve combining multiple steps and applying the core principles discussed above. For example, calculating the final price of an item after multiple discounts applied successively requires a deeper understanding of percentage computations.
Troubleshooting Common Mistakes
Several common mistakes can arise when working with percentages:
-
Incorrect decimal conversion: Failing to correctly convert a percentage to its decimal equivalent (e.g., mistaking 30% for 3.0 instead of 0.30) will lead to incorrect answers. Careful attention to decimal points is crucial.
-
Misinterpreting the problem: Carefully identifying the "part," the "whole," and the "percentage" in the problem statement is crucial. Misunderstanding the context of the problem can lead to incorrect calculations.
-
Mathematical errors: Double-checking calculations, especially in more complex problems, is vital. Simple arithmetic errors can easily skew the final result.
Conclusion
Solving "15 is 30 percent of what number?" highlights the fundamental importance of understanding percentage calculations. The three methods presented – proportions, decimal equivalents, and the percentage formula – provide flexible approaches to solving such problems. Mastering these techniques enables you to confidently tackle a wide range of percentage problems in various contexts, from everyday financial transactions to advanced scientific applications. Remember to practice regularly to reinforce your understanding and build your proficiency in this essential mathematical skill. By focusing on accuracy and understanding the underlying principles, you can confidently navigate the world of percentages.
Latest Posts
Latest Posts
-
How Many Units Are In A Milliliter
Jul 22, 2025
-
How Many Ounces In Cream Cheese Block
Jul 22, 2025
-
How Many Marshmallows In A 10 Oz Bag
Jul 22, 2025
-
How Many Cups Is A Pound Of Sour Cream
Jul 22, 2025
-
How Fast Can You Walk 1 Mile At 4mph
Jul 22, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.