15 Is 60 Of What Number
Kalali
Apr 16, 2025 · 5 min read
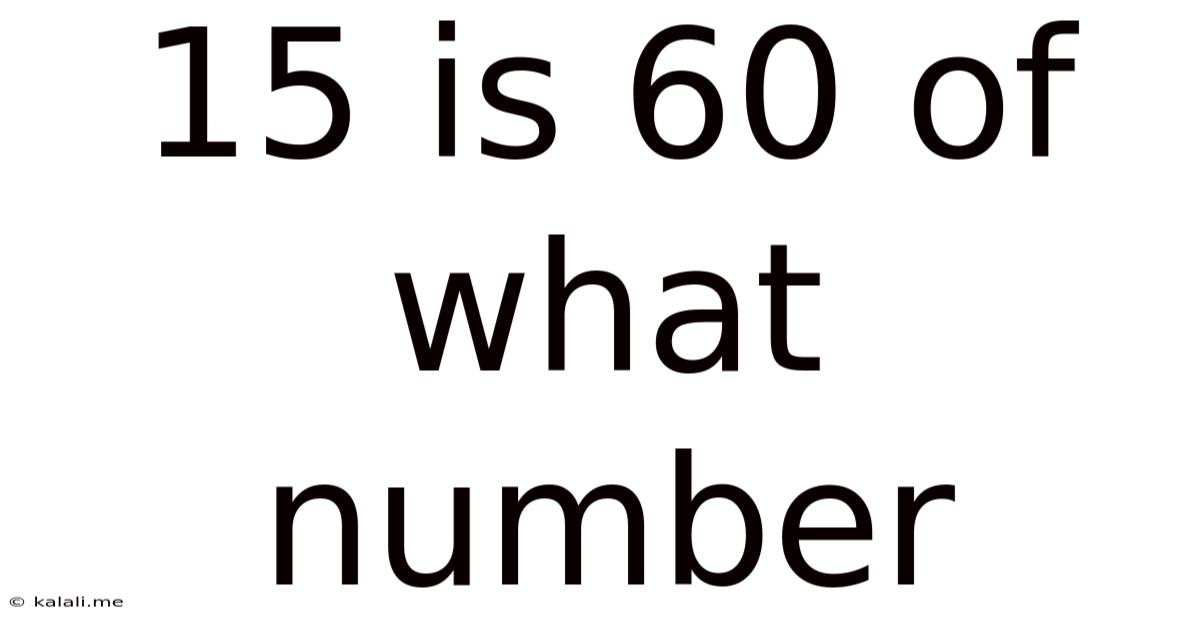
Table of Contents
15 is 60% of What Number? Unlocking the Power of Percentages
This seemingly simple question – "15 is 60% of what number?" – underpins a fundamental concept in mathematics and has wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and even baking the perfect cake. This article will not only solve the equation but will delve into the various methods for solving percentage problems, explore real-world applications, and provide you with the tools to confidently tackle similar problems in the future. Understanding percentages is key to navigating the numerical world around us, and mastering this skill opens doors to a more insightful and empowered understanding of data and information.
Understanding the Problem: Deconstructing the Percentage Equation
The question "15 is 60% of what number?" can be translated into a mathematical equation. We can represent the unknown number as 'x'. The equation then becomes:
0.60x = 15
This equation tells us that 60% (or 0.60 as a decimal) of an unknown number (x) equals 15. Our goal is to solve for 'x'. This seemingly simple equation unlocks the door to a world of percentage-based problem-solving.
Method 1: Solving the Equation Algebraically
The most straightforward method to solve for 'x' is through algebraic manipulation. We'll isolate 'x' by dividing both sides of the equation by 0.60:
x = 15 / 0.60
x = 25
Therefore, 15 is 60% of 25.
Method 2: Using Proportions
Another powerful method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can represent the problem as:
15/x = 60/100
This proportion states that the ratio of 15 to the unknown number (x) is equal to the ratio of 60 to 100 (60%). To solve for x, we can cross-multiply:
15 * 100 = 60 * x
1500 = 60x
x = 1500 / 60
x = 25
Again, we find that 15 is 60% of 25. This method provides a visual representation of the relationship between the parts and the whole, making it intuitively easier for some to grasp.
Method 3: The "Is-Of-Percent" Formula
Many students find the "Is-Of-Percent" formula helpful in solving percentage problems. The formula is:
Is / Of = Percent / 100
In our problem:
- "Is" represents the part – 15
- "Of" represents the whole – this is what we want to find (x)
- "Percent" represents the percentage – 60
Substituting these values into the formula, we get:
15 / x = 60 / 100
This is the same proportion we used in Method 2, leading us to the same solution: x = 25. This formula provides a structured approach, making it easier to plug in the known values and solve for the unknown.
Real-World Applications: Percentages in Everyday Life
The ability to solve percentage problems is a crucial life skill with applications across numerous domains:
-
Retail Sales and Discounts: Understanding percentages is essential for calculating discounts. If a store offers a 20% discount on a $50 item, you can quickly determine the final price using percentage calculations. Similarly, calculating sales tax involves understanding percentages.
-
Financial Planning and Investments: Percentages are fundamental to understanding interest rates, returns on investments, and analyzing financial statements. Calculating compound interest, for example, relies heavily on percentage calculations.
-
Data Analysis and Statistics: Percentages are used extensively to represent data in graphs, charts, and reports. Understanding percentages helps in interpreting data and drawing meaningful conclusions.
-
Scientific Calculations and Research: Many scientific calculations involve percentages, such as calculating experimental error, analyzing statistical significance, or determining concentrations of solutions.
-
Cooking and Baking: Recipes often express ingredient proportions as percentages, particularly in baking, where precision is critical. Understanding percentages ensures consistent results when scaling recipes up or down.
Beyond the Basics: Advanced Percentage Problems
While the problem "15 is 60% of what number?" is a relatively straightforward example, the principles involved extend to more complex scenarios:
-
Finding the Percentage Increase or Decrease: Calculating the percentage change between two values requires understanding percentage calculations. For example, determining the percentage increase in sales from one year to the next.
-
Calculating Percentage Points: Percentage points represent the absolute difference between two percentages. For instance, an increase from 10% to 15% is a 5-percentage-point increase, not a 50% increase.
-
Working with Multiple Percentages: Problems involving consecutive percentage changes, such as applying a discount and then a sales tax, require a step-by-step approach and a clear understanding of order of operations.
-
Solving Problems with Unknown Percentages: Sometimes, you need to find the percentage when you know the part and the whole. For example, if you sold 12 out of 20 items, what percentage did you sell? This requires reversing the process, dividing the part by the whole and multiplying by 100.
Mastering Percentages: Tips and Strategies
Here are some key strategies to improve your percentage calculation skills:
-
Practice Regularly: The more you practice, the more confident and efficient you will become in solving percentage problems. Start with simple problems and gradually work your way up to more complex scenarios.
-
Use Different Methods: Familiarize yourself with multiple methods (algebraic, proportions, "Is-Of-Percent" formula) to choose the method that suits your problem and your personal learning style.
-
Understand the Concepts: Don't just memorize formulas; focus on understanding the underlying concepts. This will allow you to apply your knowledge to a wide range of problems.
-
Check Your Work: Always check your answers to ensure accuracy. You can do this by substituting your answer back into the original equation or using a different method to verify your result.
-
Utilize Online Resources: Many online resources, such as educational websites and calculators, can provide additional practice problems and help you check your work.
Conclusion: Empowering Yourself with Percentage Proficiency
The ability to solve percentage problems is a powerful tool that extends far beyond the classroom. From managing your personal finances to analyzing data in your professional life, understanding percentages empowers you to make informed decisions and navigate the numerical world with confidence. Mastering the basic concepts and practicing regularly will equip you with a valuable skill that will serve you well throughout your life. So, the next time you encounter a percentage problem, remember the steps outlined in this article, and approach it with confidence knowing you possess the tools to find the solution. Remember, 15 is 60% of 25, and understanding how we arrived at that answer is the key to unlocking a world of numerical possibilities.
Latest Posts
Latest Posts
-
Prevent An Expressway Emergency By Merging Without
Jul 12, 2025
-
How Many Grams Of Sugar In A Pound
Jul 12, 2025
-
7am To 11am Is How Many Hours
Jul 12, 2025
-
If Your 35 What Year Was You Born
Jul 12, 2025
-
How Many Cups Is 1 Pound Of Cheese
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 60 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.