15 Of 100 Is What Percent
Kalali
Mar 11, 2025 · 5 min read
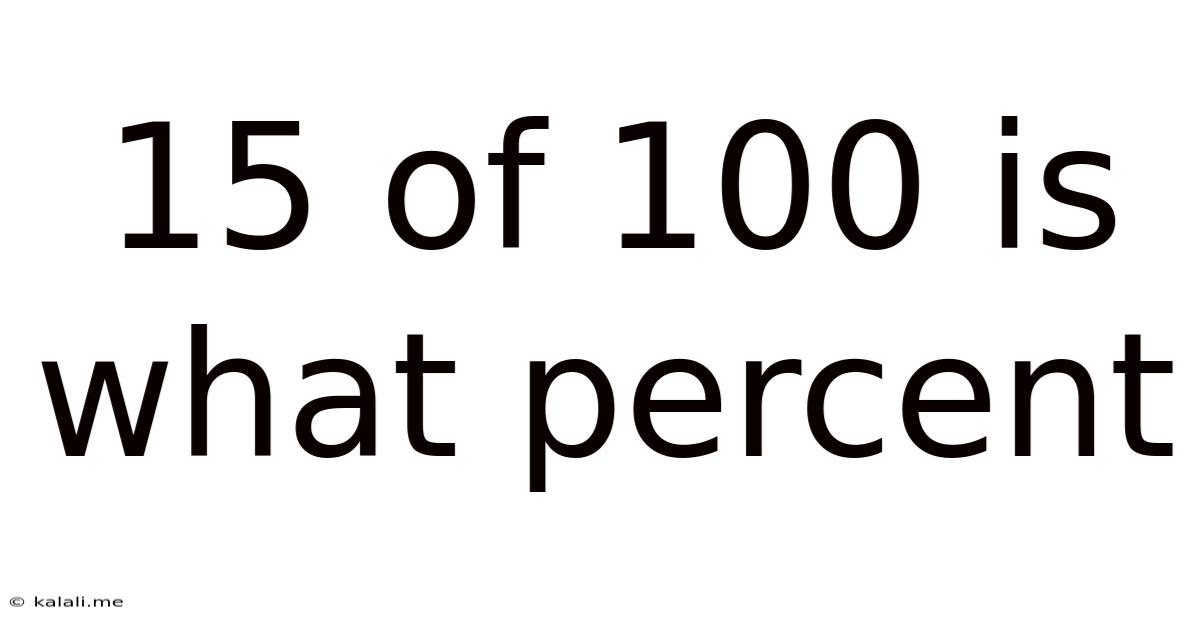
Table of Contents
15 out of 100 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and tax rates to interpreting statistics and analyzing data. This comprehensive guide will delve into the question, "15 out of 100 is what percent?", and explore the broader concept of percentage calculations, offering practical examples and tips to master this essential skill.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" or "out of 100." The symbol used to represent percentage is %. Therefore, 15% means 15 out of 100.
Calculating 15 out of 100 as a Percentage
The calculation is straightforward:
15/100 * 100% = 15%
This confirms that 15 out of 100 is indeed 15%. This is a simple example because the denominator is already 100. However, many real-world scenarios require more complex calculations.
Calculating Percentages: Different Methods
Let's explore various methods for calculating percentages, applicable to situations where the denominator isn't 100. These methods are particularly useful for understanding the broader concept and solving various percentage problems.
Method 1: Using the Fraction Method
This method involves converting the given fraction into a percentage. Let's take an example: What percentage is 30 out of 50?
- Form a fraction: 30/50
- Convert to a decimal: Divide the numerator (30) by the denominator (50): 30 ÷ 50 = 0.6
- Convert to a percentage: Multiply the decimal by 100%: 0.6 * 100% = 60% Therefore, 30 out of 50 is 60%.
Method 2: Using the Proportion Method
This method uses proportions to solve for the unknown percentage. Let's use the same example: What percentage is 30 out of 50?
- Set up a proportion: x/100 = 30/50
- Cross-multiply: 50x = 3000
- Solve for x: x = 3000 ÷ 50 = 60 Therefore, x = 60%, meaning 30 out of 50 is 60%.
Method 3: Using the Percentage Formula
The percentage formula provides a direct way to calculate percentages:
(Part/Whole) * 100% = Percentage
Where:
- Part: The specific number you're considering (e.g., 30)
- Whole: The total number (e.g., 50)
Using our example again: (30/50) * 100% = 60%
Real-World Applications of Percentage Calculations
Percentages are used extensively in various aspects of daily life and professional settings. Here are some examples:
1. Finance and Business
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Discounts and sales: Retailers use percentages to advertise discounts and sales on products. For example, a "20% off" sale means a 20% reduction in the original price.
- Tax calculations: Taxes are often calculated as a percentage of income or the value of goods and services.
- Profit margins: Businesses calculate profit margins as a percentage of revenue to assess profitability.
- Investment returns: The return on investments is often expressed as a percentage.
2. Education
- Grades and scores: Test scores, assignments, and overall grades are often expressed as percentages.
- Statistical analysis: Percentages are used extensively in educational research and data analysis.
3. Science and Technology
- Data analysis: Scientists and researchers use percentages to analyze data and present findings.
- Probability and statistics: Percentages are essential in probability calculations and statistical analysis.
4. Everyday Life
- Tip calculations: People commonly calculate tips in restaurants as a percentage of the bill.
- Recipe adjustments: When cooking, percentages can be used to adjust recipe quantities.
- Surveys and polls: Survey results are often presented as percentages.
Advanced Percentage Calculations
Beyond the basic calculations, there are several more complex percentage problems that may require a deeper understanding. These include:
1. Finding the Percentage Increase or Decrease
This involves calculating the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100%
A positive result indicates an increase, while a negative result indicates a decrease.
2. Finding the Original Value After a Percentage Change
If you know the final value and the percentage change, you can find the original value using the following formula:
Original Value = Final Value / (1 + Percentage Change) (for percentage increase)
Original Value = Final Value / (1 - Percentage Change) (for percentage decrease)
Remember to express the percentage change as a decimal (e.g., 20% becomes 0.20).
3. Calculating Percentage Points
Percentage points represent the absolute difference between two percentages. For example, an increase from 10% to 20% is a 10 percentage point increase, not a 100% increase.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with these calculations.
- Use a calculator: Calculators can significantly speed up calculations, especially with more complex problems.
- Understand the concepts: Focus on grasping the underlying principles rather than just memorizing formulas.
- Break down complex problems: Divide complex problems into smaller, manageable steps.
- Check your answers: Always double-check your calculations to ensure accuracy.
Conclusion
Understanding percentage calculations is a valuable skill with wide-ranging applications. By mastering the methods and understanding the principles outlined in this guide, you'll be equipped to tackle various percentage problems confidently, whether it's calculating discounts, analyzing data, or solving everyday problems involving proportions and percentages. Remember that 15 out of 100 is 15%, a foundational understanding that can be expanded upon to handle more intricate percentage calculations. Consistent practice and a clear understanding of the concepts will solidify your grasp of this essential mathematical tool.
Latest Posts
Latest Posts
-
What Are 2004 Pennies Worth Worlds Easyest Game
Jul 04, 2025
-
Who Did Alan Jackson Have An Affair With
Jul 04, 2025
-
How Much Is 500 Grams Of Ground Beef
Jul 04, 2025
-
1 Pound Pasta Is How Many Cups
Jul 04, 2025
-
How Many Cans Of Soda Are In A 2 Liter
Jul 04, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 100 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.