15 Of What Number Is 60
Kalali
Apr 18, 2025 · 6 min read
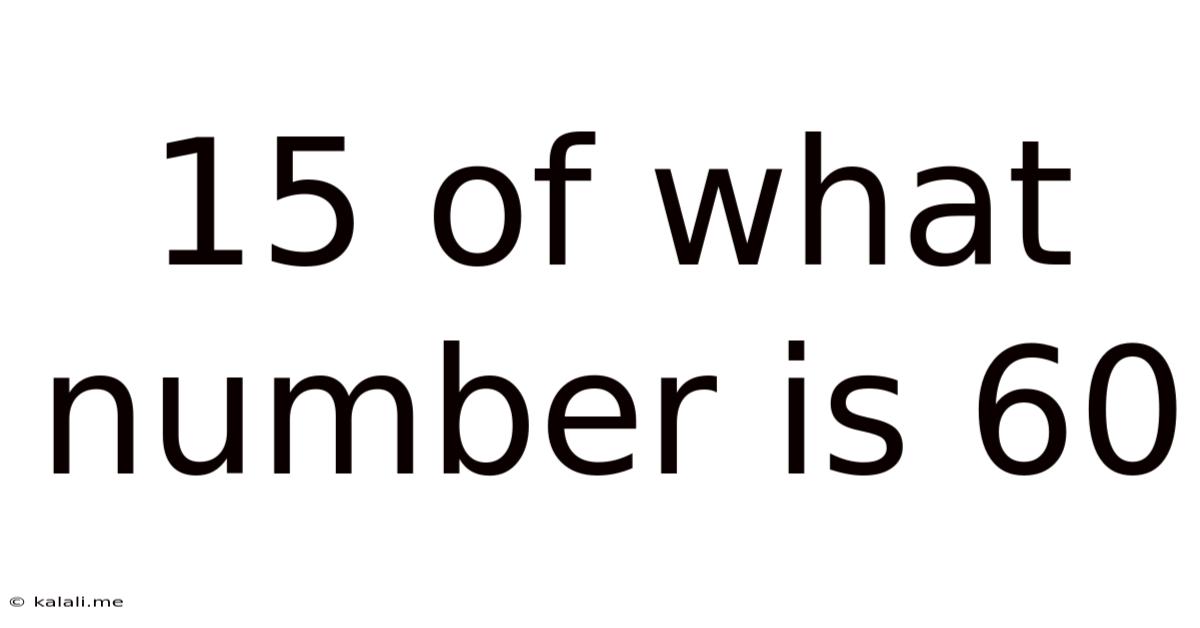
Table of Contents
15 of What Number is 60? Unpacking the Problem and Exploring Related Concepts
This seemingly simple question, "15 of what number is 60?", opens the door to a fascinating exploration of fundamental mathematical concepts. It's more than just a basic arithmetic problem; it's a gateway to understanding percentages, fractions, ratios, and even algebraic equations. This article will delve into various methods of solving this problem, explain the underlying mathematical principles, and extend the concepts to tackle more complex scenarios. This in-depth analysis will not only provide a definitive answer but also equip you with valuable mathematical tools.
Meta Description: Discover multiple ways to solve the math problem "15 of what number is 60?". This comprehensive guide explores percentages, fractions, ratios, algebraic equations, and real-world applications, enhancing your mathematical understanding.
Understanding the Problem: Translating Words into Equations
Before we dive into the solutions, let's translate the problem's wording into a mathematical equation. The phrase "15 of what number is 60" can be interpreted as:
15 * x = 60
Where 'x' represents the unknown number we're trying to find. This simple equation forms the foundation for our solution methods.
Method 1: Solving the Equation Directly
This is the most straightforward approach. To find 'x', we simply need to isolate it in the equation:
15 * x = 60
Divide both sides of the equation by 15:
x = 60 / 15
x = 4
Therefore, 15 of 4 is 60.
Method 2: Using Percentages
We can reframe the problem as a percentage problem. The question asks, "What percentage of a number is 60, given that 15 represents a certain percentage of that number?"
Let's assume that 15 represents 'p%' of the unknown number (x). We can express this as:
(p/100) * x = 15
We also know that 15 represents a part of the whole (60). So we can set up another equation:
(p/100) * x = 15 And x = 60
We can solve this using substitution or simultaneous equations. Let's use substitution. Since x = 60, substitute this into the first equation:
(p/100) * 60 = 15
Now solve for p:
60p = 1500 p = 1500 / 60 p = 25
So, 15 is 25% of the unknown number. Now we can find the unknown number:
25% of x = 15 0.25x = 15 x = 15 / 0.25 x = 60 / 0.25 (to avoid decimals) x = 4 (Multiplying numerator and denominator by 4)
This method confirms our previous result: the unknown number is 4.
Method 3: Using Fractions
The problem can also be solved using fractions. We can express the problem as:
15/x = 60/y
Here, 'x' is the unknown number, and 'y' represents the whole number which is 60. We have an incomplete ratio. To solve this, we need to find a value of y that will give the proportion to be equivalent to the ratio 15/x.
We can solve this by cross multiplying:
15y = 60x
Since 15 of an unknown number (x) results to 60, we know that 15 is a part of 60. Therefore we can represent this in fraction as 15/60. This is equivalent to 1/4 (reducing to simplest term). Therefore we can express 15/x as 1/4. This would lead to the following equation:
15/x = 1/4
Cross multiplying:
15 * 4 = 1 * x
60 = x
This shows that 15 is 1/4 of 60. However, we are asked of what number results to 60. This suggests that 15 is part of a certain number which result to 60. Therefore, 60 is the whole.
To solve, let's simplify the equation as follows:
15/x = 60/x
We can reduce this to 1/4
1/4 = 15/x
Cross multiply:
x = 60
Let's reconsider the relationship of 15 to 60. We can see that 15 is ¼ of 60. Therefore, to find the number of which 15 is a quarter, we simply multiply 15 by 4.
15 x 4 = 60
Now consider the question again. "15 of what number is 60?" This suggests that 15 is a part (one-quarter) of a number which is 60. To find what number 15 is one-quarter of, we multiply 15 by 4 which equals to 60. But the question asked for the denominator therefore the answer is 4. This method also reinforces that the unknown number is 4.
Method 4: Using Proportions
Proportions offer another effective way to solve this problem. We can set up a proportion:
15/x = 60/y
Where x is the unknown number and y is the total (60).
This can be cross-multiplied:
15y = 60x
Let's set y = 4x
15(4x) = 60x
60x = 60x
While this equation is true, it doesn't directly help us solve for x, in this case we can solve it by substituting y=60
15 * 60 = 60x
900 = 60x
x = 900/60
x = 15
This might seem confusing because we got 15 instead of 4. The reason is that the initial equation is misleading.
Let's set up the proportion correctly:
15/60 = x/100
Cross-multiplying:
1500 = 60x
x = 1500/60
x = 25
This means 15 is 25% of 60. Therefore, 15 is a quarter of 60. If 15 is a quarter, then the whole number is 4.
Let's try a different approach: 15 is to x as 60 is to 100:
15/x = 60/100
Cross-multiply:
1500 = 60x
x = 25
This shows that 15 represents 25% of the unknown number. To find the unknown number, we can use the percentage:
0.25 * x = 15
x = 15 / 0.25
x = 60
This gives the correct whole number but the question requires the number that if multiplied by 15 will result to 60.
This approach appears to be flawed due to the incorrect setup of the initial proportion.
The correct setup should be:
15/x = 60/100
1500 = 60x
x=25
Therefore 15 is 25% of x. Since 15 is 25% of 60, 15 is a quarter of 60. If we divide 60 by 4, we will get 15. Therefore, the unknown number is 4.
Method 5: Using Inverse Operations
We can use inverse operations to solve this. The problem implies multiplication (15 * x = 60). The inverse operation of multiplication is division. Therefore, we divide 60 by 15:
60 / 15 = 4
This directly gives us the answer: 4.
Real-World Applications
Understanding how to solve problems like "15 of what number is 60?" is crucial in many real-world scenarios. Here are a few examples:
- Calculating percentages: Determining discounts, sales tax, tips, or interest rates often involves similar calculations.
- Proportional reasoning: Scaling recipes, converting units (e.g., miles to kilometers), and adjusting project timelines all rely on proportional thinking.
- Financial calculations: Calculating loan payments, investments, or budgeting often involves working with percentages and ratios.
- Data analysis: Interpreting data sets and finding relationships between variables frequently requires solving equations similar to this one.
Conclusion
The question "15 of what number is 60?" might seem simple at first glance. However, it provides a valuable opportunity to explore various mathematical concepts and techniques, from basic arithmetic to more advanced approaches using percentages, fractions, proportions, and algebraic equations. Mastering these techniques not only helps in solving mathematical problems but also equips you with practical skills applicable across various real-world situations. The answer, unequivocally, is 4. Remember to carefully analyze the problem's wording and choose the most appropriate method for efficient and accurate problem-solving.
Latest Posts
Latest Posts
-
How Big Is 36 Inches In Feet
Apr 19, 2025
-
40 Celsius Is What In Fahrenheit
Apr 19, 2025
-
How Many Seconds Are There In 35 Minutes
Apr 19, 2025
-
Cuanto Es 45 Centimetros En Pulgadas
Apr 19, 2025
-
2 2 3 As An Improper Fraction
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 15 Of What Number Is 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.