15 Out Of 30 As A Percentage
Kalali
Apr 24, 2025 · 5 min read
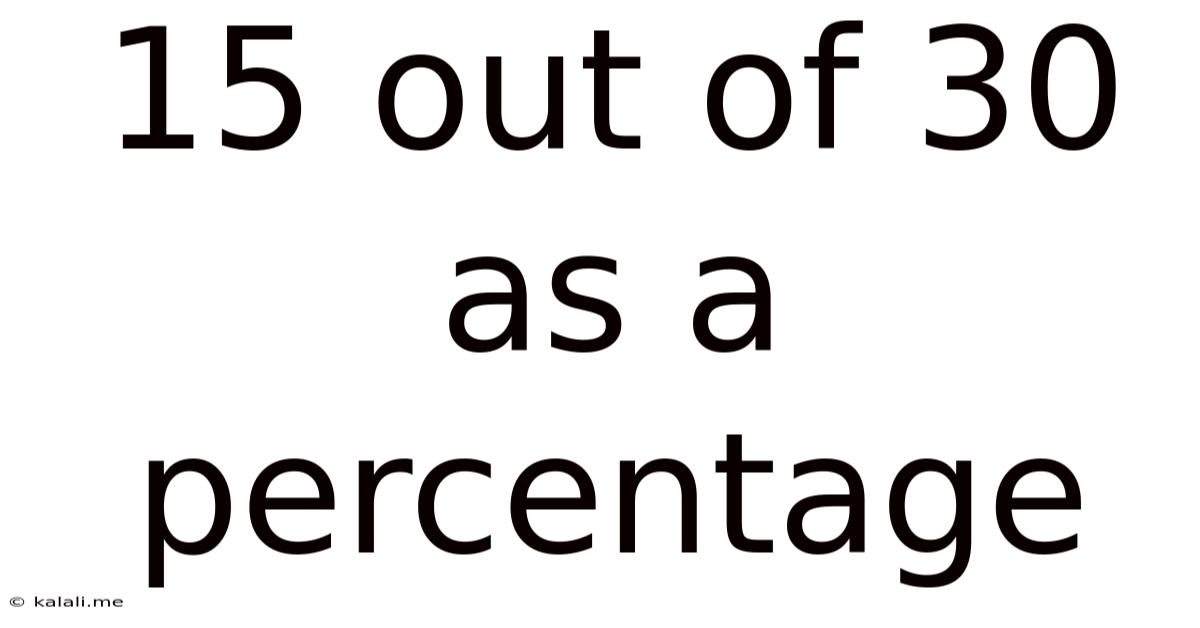
Table of Contents
15 out of 30 as a Percentage: A Comprehensive Guide to Percentage Calculations and Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from academic assessments and financial transactions to understanding statistical data and everyday decision-making. This article delves deep into the process of determining what 15 out of 30 represents as a percentage, explaining the underlying method, offering alternative approaches, and exploring practical scenarios where this type of calculation is crucial. Understanding this simple calculation opens the door to a broader understanding of percentage-based analysis and problem-solving.
What is a Percentage?
Before diving into the calculation, let's establish a clear understanding of what a percentage actually is. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote a percentage. It essentially represents a part of a whole, with the whole always being considered as 100%. For example, 50% means 50 out of 100, or half.
Calculating 15 out of 30 as a Percentage: The Basic Method
The most straightforward way to calculate 15 out of 30 as a percentage involves a two-step process:
-
Formulate the Fraction: Represent the given numbers as a fraction: 15/30. This fraction signifies 15 parts out of a total of 30 parts.
-
Convert the Fraction to a Percentage: To convert this fraction to a percentage, multiply the fraction by 100%:
(15/30) * 100% = 50%
Therefore, 15 out of 30 is equal to 50%.
Alternative Methods for Percentage Calculation
While the above method is the most common and easiest to understand, several other methods can be used to arrive at the same result. These methods can be particularly useful depending on the complexity of the problem or your personal preference:
-
Simplifying the Fraction: Before multiplying by 100%, you can simplify the fraction 15/30. Both the numerator (15) and the denominator (30) are divisible by 15. Simplifying gives you 1/2. Multiplying 1/2 by 100% still results in 50%. This method is especially helpful when dealing with larger numbers that can be simplified.
-
Using Decimal Equivalents: Convert the fraction 15/30 to a decimal by performing the division: 15 ÷ 30 = 0.5. Then, multiply the decimal by 100% to obtain the percentage: 0.5 * 100% = 50%.
-
Using a Calculator: Modern calculators often have a percentage function (%) that simplifies the calculation. Simply enter 15, press the division key (/), enter 30, and then press the percentage key (%) to directly obtain the result: 50%.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages has far-reaching applications across numerous fields:
Academic Performance:
- Grade Calculation: If a student answers 15 out of 30 questions correctly on a test, their score is 50%. This is a fundamental aspect of assessing student performance. Understanding percentages helps students, teachers, and parents track progress and identify areas for improvement.
- Exam Results: Percentage calculations are crucial for interpreting exam results, comparing performance across different subjects, and determining overall academic standing. This is particularly relevant in standardized testing where scores are often represented as percentages.
Finance and Business:
- Profit and Loss: Businesses use percentages extensively to calculate profit margins, loss percentages, and rates of return on investments. Understanding these calculations is vital for financial planning and decision-making.
- Discounts and Sales: Retailers frequently advertise discounts as percentages (e.g., a 20% off sale). Consumers need to understand percentage calculations to determine the actual price after the discount.
- Interest Rates: Interest rates on loans, savings accounts, and investments are usually expressed as percentages. Accurate percentage calculations are essential for understanding the financial implications of these rates.
- Tax Calculations: Sales tax, income tax, and other taxes are often calculated as percentages of the total amount.
Statistics and Data Analysis:
- Data Representation: Percentages are widely used to represent data in charts, graphs, and reports, making it easier to visualize and understand trends and patterns.
- Statistical Inference: Percentage calculations play a key role in various statistical analyses, including hypothesis testing and confidence intervals.
Everyday Life:
- Tip Calculation: Calculating a tip at a restaurant often involves determining a percentage (e.g., 15% or 20%) of the total bill.
- Ingredient Ratios: Cooking recipes often specify ingredient ratios as percentages (e.g., 60% flour, 40% water).
- Survey Results: Survey data is frequently presented as percentages to illustrate the distribution of responses and identify key trends.
Advanced Applications:
Beyond these basic applications, percentage calculations form the basis of more complex mathematical concepts and formulas:
- Compound Interest: Calculating compound interest involves repeated percentage calculations over time.
- Growth Rates: Tracking the growth or decline of populations, economies, or investments often relies on percentage changes.
- Probability: Probabilities are often expressed as percentages, representing the likelihood of an event occurring.
Beyond the Basics: Understanding Percentage Change
While this article primarily focuses on calculating a percentage from a given ratio, understanding percentage change is equally important. Percentage change measures the relative difference between two values. The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100%
For example, if a value increases from 20 to 30, the percentage change is:
[(30 - 20) / 20] * 100% = 50% increase
Conversely, if a value decreases from 30 to 20, the percentage change is:
[(20 - 30) / 30] * 100% = -33.33% decrease
Understanding percentage change is crucial for interpreting trends, comparing data over time, and making informed decisions based on changes in values.
Conclusion:
Calculating 15 out of 30 as a percentage—resulting in 50%—is a simple yet fundamental calculation with far-reaching applications. Mastering this skill unlocks a deeper understanding of percentage-based analysis, enabling more effective problem-solving across diverse fields. From academic assessments and financial management to statistical analyses and everyday tasks, the ability to calculate and interpret percentages is an invaluable skill for anyone seeking to navigate the complexities of numerical data and make informed decisions. Remember to practice regularly and explore the different methods to find the approach that best suits your needs and preferences. The more you work with percentages, the more intuitive and effortless the process will become.
Latest Posts
Latest Posts
-
17 Out Of 18 Is What Percent
Apr 25, 2025
-
Least Common Multiple Of 15 And 18
Apr 25, 2025
-
What Is 23 5 Cm In Inches
Apr 25, 2025
-
How Can Reduced Precipitation Lead To Limited Water Availability
Apr 25, 2025
-
Is Probability A Percent Or Decimal
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about 15 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.