150 Is What Percent Of 50
Kalali
Apr 24, 2025 · 5 min read
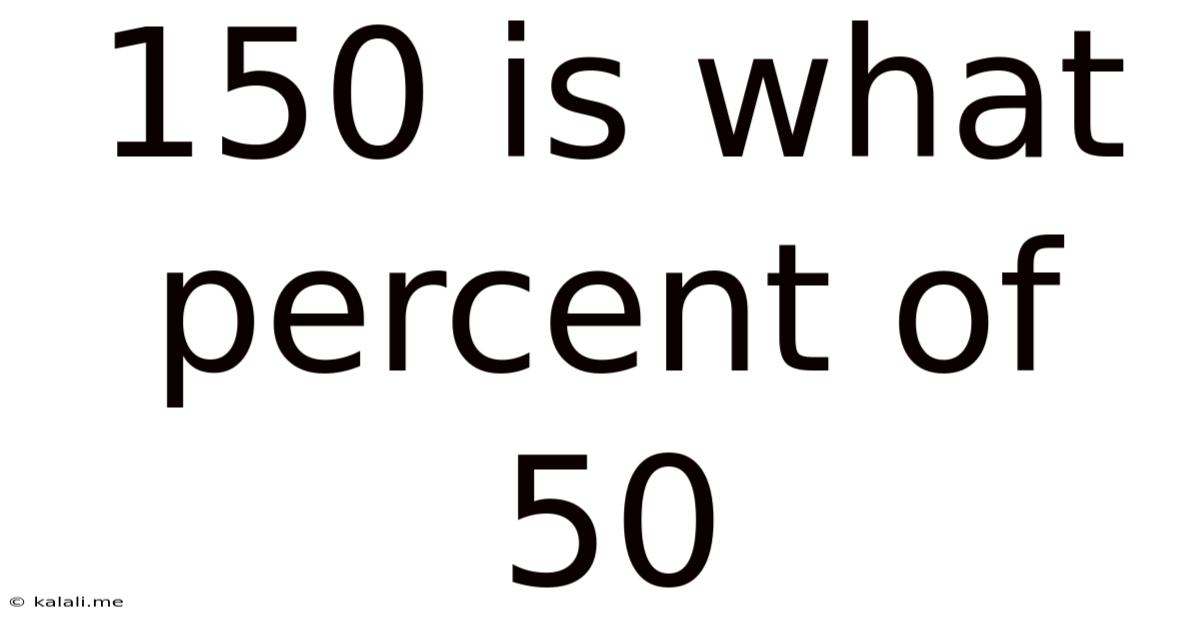
Table of Contents
150 is What Percent of 50? Understanding Percentage Calculations and Their Applications
This seemingly simple question, "150 is what percent of 50?", opens the door to a vast world of percentage calculations, their practical applications, and the underlying mathematical principles. While the answer might seem counterintuitive at first glance – a larger number cannot be a percentage of a smaller number without exceeding 100% – understanding the process reveals valuable insights into how percentages work and their relevance in various fields. This article will not only provide the solution but also delve into the methodology, explain related concepts, and illustrate its real-world applications.
Meta Description: Learn how to calculate percentages effectively. This comprehensive guide tackles the question "150 is what percent of 50?" and explains the underlying mathematical principles with practical examples from various fields.
The immediate answer to the question “150 is what percent of 50?” is 300%. But let's understand how we arrive at this answer and explore the broader context of percentage calculations.
Understanding Percentages: The Basics
Percentages are a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). A percentage is a dimensionless number; it doesn't have units like meters or kilograms. Instead, it represents a proportion or ratio.
For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This fundamental understanding is crucial for solving percentage problems.
Calculating Percentages: The Formula
The basic formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
Where:
- Part: The number you're interested in expressing as a percentage of the whole.
- Whole: The total number or the base amount.
- Percentage: The resulting percentage value.
In our problem, "150 is what percent of 50?", we have:
- Part = 150
- Whole = 50
Applying the formula:
(150 / 50) * 100% = 300%
Therefore, 150 is 300% of 50. This result signifies that 150 is three times larger than 50.
Interpreting the Result: Beyond the Calculation
The result of 300% might seem unusual at first because we typically associate percentages with values between 0% and 100%. However, percentages can exceed 100%. This indicates that the "part" is greater than the "whole." This scenario is common in various real-world contexts:
-
Growth and Increase: Imagine a business whose revenue increased from 50 units to 150 units. The increase is 100 units, representing a 200% growth compared to the initial 50 units. Adding this 200% growth to the original 100% gives us the 300% figure.
-
Comparisons and Ratios: Percentages are frequently used to compare different quantities. In this case, 150 is three times larger than 50; hence, the 300% representation highlights this significant difference.
-
Financial Statements: Financial reports often use percentages exceeding 100% to illustrate growth, profit margins that are significantly above the initial investment or other key performance indicators.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous across numerous disciplines:
-
Finance: Calculating interest rates, returns on investments, profit margins, discounts, tax rates, and more all rely heavily on percentage calculations.
-
Business: Analyzing sales figures, market share, growth rates, and cost-benefit ratios. Understanding percentage changes is essential for making informed business decisions.
-
Science: Expressing experimental results, statistical analysis, and data representation often involve percentages. For instance, expressing the concentration of a solution or the percentage of a certain element in a compound.
-
Everyday Life: Calculating tips, discounts, sales tax, and understanding proportions in recipes or measurements.
Solving Related Percentage Problems
Understanding the fundamental formula allows you to tackle a variety of percentage problems:
1. Finding the Part: If you know the percentage and the whole, you can find the part:
- Formula: (Percentage/100) * Whole = Part
Example: What is 25% of 80? (25/100) * 80 = 20
2. Finding the Whole: If you know the percentage and the part, you can find the whole:
- Formula: (Part / Percentage) * 100 = Whole
Example: 15 is 30% of what number? (15 / 30) * 100 = 50
Advanced Percentage Concepts: Percentage Change and Percentage Point Difference
Beyond basic percentage calculations, understanding percentage change and percentage point difference is crucial for interpreting data accurately:
1. Percentage Change: This measures the relative change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100% = Percentage Change
Example: If sales increased from 100 to 150, the percentage change is [(150 - 100) / 100] * 100% = 50%
2. Percentage Point Difference: This represents the absolute difference between two percentages. It's not a percentage change, but rather the difference between two percentage values.
Example: If the interest rate increases from 5% to 8%, the percentage point difference is 3 percentage points. This is different from saying the interest rate increased by 60% [(8-5)/5 * 100% = 60%], which is the percentage change.
Common Mistakes in Percentage Calculations
Avoid these common pitfalls:
-
Confusing Percentage Change and Percentage Point Difference: Clearly differentiate between these two concepts.
-
Incorrectly Applying the Formula: Double-check your calculations and ensure you're using the correct formula for the specific problem.
-
Ignoring the Units: Pay attention to the units of measurement and ensure consistency throughout the calculation.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple steps in a calculation. Round off only at the final step.
Conclusion: The Power of Percentage Calculations
The seemingly simple question, "150 is what percent of 50?" highlights the importance of understanding percentage calculations. This article provides a comprehensive overview of the underlying mathematics, interpretation of results (including percentages exceeding 100%), practical applications across diverse fields, and related concepts. Mastering percentage calculations equips you with a fundamental skill applicable in numerous aspects of life, from everyday finances to complex business analyses. By avoiding common errors and understanding the subtleties, you can harness the power of percentages to make informed decisions and effectively interpret data.
Latest Posts
Latest Posts
-
2 5 Kg Is How Many Grams
Apr 24, 2025
-
34 Degrees Celsius Converted To Fahrenheit
Apr 24, 2025
-
What Processes Changed The Earths Environment During Precambrian Time
Apr 24, 2025
-
What Is 9 13 As A Percent
Apr 24, 2025
-
What Is 2 5 Oz In A Measuring Cup
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about 150 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.