16 Is What Percent Of 20
Kalali
Mar 29, 2025 · 4 min read
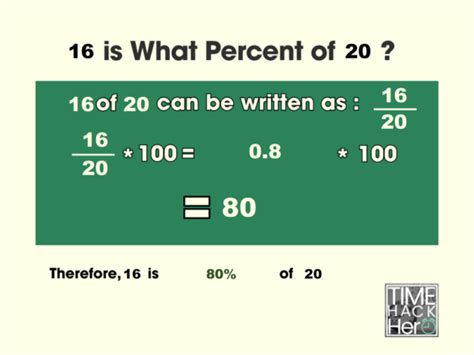
Table of Contents
16 is What Percent of 20? A Deep Dive into Percentage Calculations
This seemingly simple question, "16 is what percent of 20?", opens the door to a world of practical applications for percentages. Understanding how to calculate percentages is crucial in various aspects of life, from budgeting and finance to sales, discounts, and even understanding statistical data. This article will not only answer the question directly but will also delve into the underlying concepts, provide multiple methods for solving similar problems, and explore real-world examples to solidify your understanding.
Understanding Percentages
Before we tackle the specific problem, let's establish a solid foundation in percentage calculations. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of 100." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Terms:
- Part: The value that represents a portion of the whole. In our example, 16 is the part.
- Whole: The total value to which the part is compared. In our example, 20 is the whole.
- Percentage: The fraction expressed as a part of 100. This is what we need to find.
Calculating "16 is What Percent of 20?"
There are several ways to solve this percentage problem. We'll explore three common methods:
Method 1: Using the Formula
The most straightforward method involves using the percentage formula:
(Part / Whole) x 100% = Percentage
-
Identify the parts: Part = 16, Whole = 20
-
Substitute into the formula: (16 / 20) x 100% = Percentage
-
Calculate: (0.8) x 100% = 80%
Therefore, 16 is 80% of 20.
Method 2: Proportions
This method uses the concept of equivalent ratios. We can set up a proportion:
16/20 = x/100
Where 'x' represents the unknown percentage.
To solve for x, we cross-multiply:
16 * 100 = 20 * x
1600 = 20x
x = 1600 / 20
x = 80
Therefore, 16 is 80% of 20.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
-
Form the fraction: 16/20
-
Convert to a decimal: 16 divided by 20 equals 0.8
-
Multiply by 100%: 0.8 x 100% = 80%
Therefore, 16 is 80% of 20.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in many real-world scenarios. Here are some examples:
1. Sales and Discounts:
Imagine a shirt originally priced at $20 is on sale for $16. Using the methods above, we've already determined that the discount is 80% of the original price. However, to find the percentage discount, we calculate the discount amount ($20 - $16 = $4) and then use the formula:
(Discount Amount / Original Price) x 100% = Percentage Discount
($4 / $20) x 100% = 20%
The shirt is discounted by 20%.
2. Financial Calculations:
Percentages are fundamental in finance. Calculating interest rates, returns on investment, and understanding loan terms all involve percentage calculations. For example, if you invest $1000 and earn $80 in interest, the return on investment is:
($80 / $1000) x 100% = 8%
3. Statistics and Data Analysis:
Percentages are used extensively in statistics to represent proportions within data sets. For example, if a survey shows that 16 out of 20 people prefer a certain product, this translates to an 80% preference rate.
4. Grade Calculations:
In education, percentages are used to express grades and scores. If you answer 16 out of 20 questions correctly on a test, your score is 80%.
5. Tax Calculations:
Sales tax, income tax, and other forms of taxation often involve percentage calculations. For instance, a 5% sales tax on a $20 item would be $1.
Beyond the Basics: More Complex Percentage Problems
While the "16 is what percent of 20?" problem is relatively straightforward, percentage calculations can become more complex. Here are some examples and how to approach them:
1. Finding the Whole:
Problem: 80% of what number is 16?
Solution: We can adapt the formula:
(Percentage/100) x Whole = Part
(80/100) x Whole = 16
0.8 x Whole = 16
Whole = 16 / 0.8
Whole = 20
2. Finding the Part:
Problem: What is 80% of 20?
Solution:
(Percentage/100) x Whole = Part
(80/100) x 20 = 16
3. Percentage Increase/Decrease:
Problem: A price increases from $20 to $24. What is the percentage increase?
Solution:
-
Find the difference: $24 - $20 = $4
-
Calculate the percentage increase: ($4 / $20) x 100% = 20%
Conclusion: Mastering Percentages for Everyday Life
The ability to confidently calculate percentages is a valuable skill applicable across numerous domains. This article has explored the fundamental concepts, provided multiple methods for solving percentage problems, and showcased practical examples to illustrate its relevance in everyday life. From managing personal finances to interpreting statistical data, mastering percentages empowers you to make informed decisions and navigate a world filled with numerical information. Remember the basic formula, practice different methods, and apply your knowledge to real-world situations to truly internalize the concept of percentages. With consistent practice, you'll find that percentage calculations become second nature.
Latest Posts
Latest Posts
-
What Percent Of 40 Is 15
Mar 31, 2025
-
How Many Calories In A 1 Gram Of Fat
Mar 31, 2025
-
Cuanto Es 100 Pies En Metros
Mar 31, 2025
-
How Much Is 6 Liters In Gallons
Mar 31, 2025
-
43 Grados Centigrados Convertirlos A Fahrenheit
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 16 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
