17 Is What Percent Of 25
Kalali
Apr 08, 2025 · 5 min read
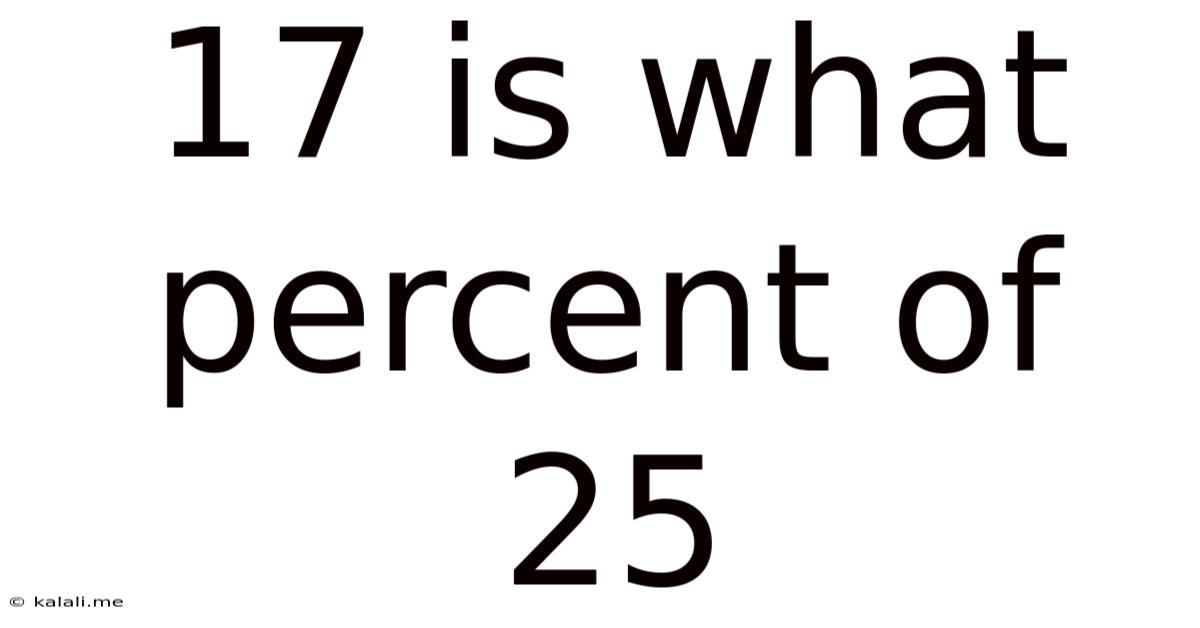
Table of Contents
17 is What Percent of 25? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "17 is what percent of 25?", opens the door to a world of percentage calculations crucial for everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This comprehensive guide will not only answer this specific question but also equip you with the knowledge and skills to tackle any percentage problem with confidence. We'll explore multiple methods, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Meta Description: Learn how to calculate percentages with this in-depth guide. We'll solve "17 is what percent of 25?" using multiple methods and explore practical applications of percentage calculations in everyday life.
Understanding Percentages: The Basics
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Percentages are used extensively to represent proportions, changes, and ratios in various contexts. Understanding percentages is essential for interpreting data, making comparisons, and solving numerous real-world problems.
Method 1: Using the Percentage Formula
The most straightforward way to solve "17 is what percent of 25?" is to use the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 17
- Whole: 25
Substituting these values into the formula:
(17 / 25) * 100% = 68%
Therefore, 17 is 68% of 25.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
17 / 25 = x / 100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
17 * 100 = 25 * x
1700 = 25x
x = 1700 / 25
x = 68
Therefore, 17 is 68% of 25.
Method 3: Using Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100%.
First, we express the problem as a fraction: 17/25.
Next, we convert the fraction to a decimal by performing the division: 17 ÷ 25 = 0.68
Finally, we multiply the decimal by 100% to express it as a percentage: 0.68 * 100% = 68%
Thus, 17 is 68% of 25.
Practical Applications of Percentage Calculations
The ability to calculate percentages has widespread applications in various fields:
1. Finance:
- Interest rates: Calculating simple and compound interest on loans, savings accounts, and investments. Understanding interest rates is crucial for making informed financial decisions.
- Discounts and sales: Determining the final price of an item after applying a discount percentage. This is essential for budget planning and smart shopping.
- Taxes: Calculating sales tax, income tax, and other taxes based on a percentage of earnings or purchases. Tax calculations are fundamental for responsible financial management.
- Investment returns: Evaluating the performance of investments by calculating percentage returns or losses. This allows investors to track their portfolio's growth and make adjustments as needed.
2. Business:
- Profit margins: Calculating the percentage of profit earned on sales. Profit margins are vital for assessing business profitability and making pricing decisions.
- Market share: Determining a company's market share by expressing its sales as a percentage of the total market sales. Market share analysis helps companies understand their competitive position.
- Growth rates: Measuring the percentage increase or decrease in sales, revenue, or other key metrics over time. Growth rates provide insights into business performance and trends.
- Cost analysis: Calculating the percentage of total costs attributed to different aspects of production or operations. This information is vital for optimizing efficiency and reducing costs.
3. Education:
- Grades and scores: Converting numerical scores on tests and assignments to percentages. This allows for consistent evaluation and comparison of student performance.
- Statistical analysis: Using percentages to represent data and trends in educational research and assessment. Percentages help educators understand patterns and make informed decisions.
4. Science:
- Data representation: Expressing scientific data and results as percentages to improve clarity and facilitate comparisons. Percentages are widely used in scientific reporting and data visualization.
- Concentration calculations: Determining the concentration of a substance as a percentage of the total solution or mixture. Concentration calculations are fundamental in chemistry and other scientific disciplines.
5. Everyday Life:
- Tipping: Calculating a gratuity based on a percentage of the bill amount. Tipping is a common social practice in many cultures.
- Cooking and baking: Adjusting ingredient quantities based on percentage changes in recipe size. Accurate percentage calculations are important for successful cooking and baking.
- Shopping: Comparing prices and determining the best value for money by calculating percentage discounts and savings.
Advanced Percentage Calculations
While the basic percentage formula serves as a foundation, there are several more advanced applications of percentage calculations that are useful to know:
- Percentage Increase/Decrease: Calculating the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100%. The formula for percentage decrease is similar, but the result will be negative.
- Percentage Points: Understanding the difference between percentage change and percentage points. A change of 10 percentage points is a different value than a 10% increase.
- Compound Percentage Growth: Calculating the final value after repeated percentage increases over time. This is often used in finance when calculating compound interest.
These advanced concepts are especially important when working with financial data, economic indicators, or any situation where understanding the growth or decline of values over time is essential.
Troubleshooting Common Percentage Mistakes
Common mistakes that people often make when calculating percentages include:
- Incorrect order of operations: Remember to perform the division before multiplying by 100%.
- Using the wrong values: Carefully identify the "part" and the "whole" in the problem.
- Misinterpreting percentage change: Distinguishing between percentage change and percentage points.
- Rounding errors: Be aware that rounding intermediate calculations can lead to inaccuracies in the final result.
Conclusion
Mastering percentage calculations is a valuable skill applicable to various aspects of life. By understanding the fundamental concepts and formulas, practicing different methods, and being aware of common pitfalls, you'll be equipped to tackle any percentage problem with confidence. This guide provides a comprehensive foundation, enabling you to not only solve problems like "17 is what percent of 25?" but also to apply your knowledge to more complex percentage calculations in diverse real-world situations. Remember to practice regularly to solidify your understanding and enhance your problem-solving skills.
Latest Posts
Latest Posts
-
How Do You Eliminate The Parameter
Apr 17, 2025
-
How Many Parallel Sides Does Trapezoid Have
Apr 17, 2025
-
How Much Is 64 Ounces In Cups
Apr 17, 2025
-
Back To Back Stem And Leaf Diagram
Apr 17, 2025
-
What Percentage Is 11 Out Of 18
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 17 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.