17 Out Of 30 As A Percentage
Kalali
Mar 09, 2025 · 4 min read
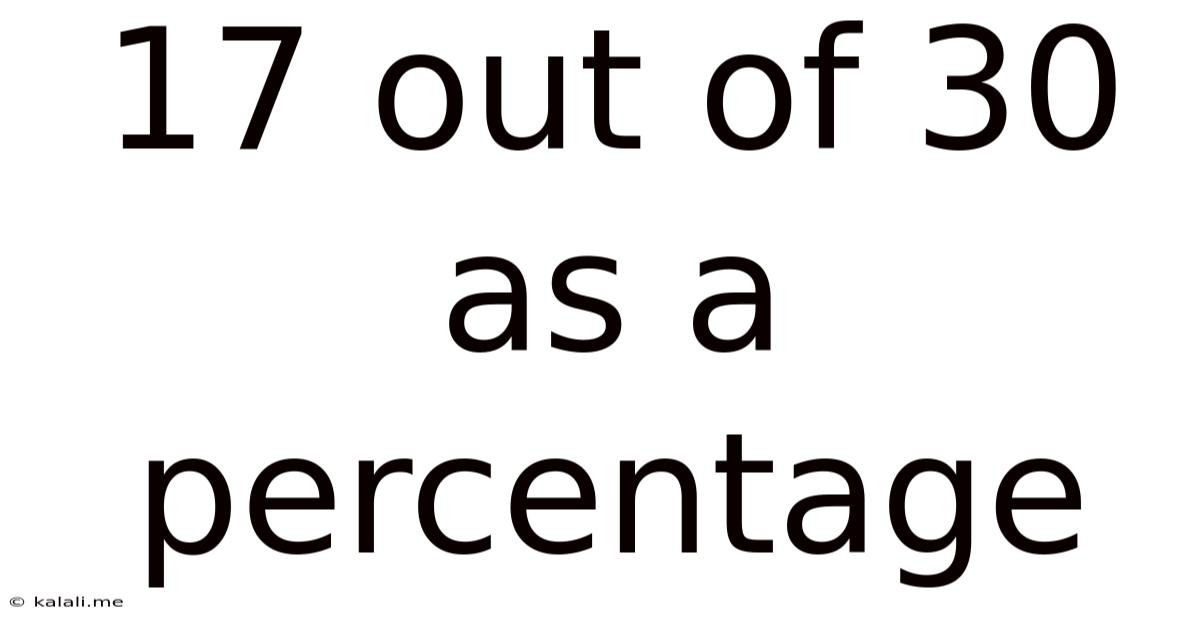
Table of Contents
17 out of 30 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific calculations. This comprehensive guide delves into the process of calculating percentages, specifically addressing the question: "What is 17 out of 30 as a percentage?" We'll explore various methods, provide practical examples, and offer tips for mastering percentage calculations.
Understanding Percentages: The Basics
A percentage represents a fraction of 100. The term "percent" originates from the Latin "per centum," meaning "out of a hundred." Therefore, expressing a value as a percentage essentially translates it into a proportion relative to 100.
For instance, 50% means 50 out of 100, which simplifies to one-half or 0.5 as a decimal. Understanding this fundamental relationship is crucial for all percentage calculations.
Calculating 17 out of 30 as a Percentage: The Three Methods
There are three primary methods to calculate 17 out of 30 as a percentage:
Method 1: The Fraction Method
This method involves expressing the given numbers as a fraction and then converting the fraction into a percentage.
-
Form a fraction: Express "17 out of 30" as a fraction: 17/30.
-
Convert to decimal: Divide the numerator (17) by the denominator (30): 17 ÷ 30 = 0.566666...
-
Convert to percentage: Multiply the decimal by 100: 0.566666... × 100 = 56.6666...%
-
Round to desired precision: Depending on the required level of accuracy, round the percentage. Rounding to two decimal places, we get 56.67%.
Method 2: The Proportion Method
This method utilizes the concept of proportions to solve for the percentage.
-
Set up a proportion: We can represent the problem as a proportion: 17/30 = x/100, where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiply the terms: 17 * 100 = 30 * x
-
Solve for x: This gives us 1700 = 30x. Divide both sides by 30: x = 1700/30 = 56.6666...
-
Convert to percentage: The result, 56.6666..., is already expressed as a percentage. Rounding to two decimal places, we again obtain 56.67%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply input 17 ÷ 30 and then multiply the result by 100 to obtain the percentage. This method offers the quickest and often most accurate result, particularly for more complex calculations. The answer will be 56.67% when rounded to two decimal places.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential in numerous real-world scenarios. Here are a few examples:
-
Academic Performance: If a student answers 17 questions correctly out of 30 on a test, their score is 56.67%. This helps assess their understanding of the subject matter.
-
Sales and Discounts: A store offering a discount of 17% on an item priced at $30 would reduce the price by $5.10 ($30 * 0.17 = $5.10).
-
Financial Calculations: Calculating interest rates, tax percentages, and profit margins all require understanding and applying percentage calculations.
-
Statistical Analysis: Percentages are frequently used to represent data in surveys, polls, and scientific research, allowing for easier comparison and interpretation.
-
Recipe Scaling: Adjusting recipe ingredients proportionally requires accurate percentage calculations to maintain the correct ratios.
Beyond the Basics: More Complex Percentage Problems
While calculating 17 out of 30 as a percentage is relatively straightforward, the concept expands to more complex scenarios. Let's consider some variations:
-
Calculating the percentage increase or decrease: If a quantity changes from 30 to 17, we can calculate the percentage decrease as follows: [(30 - 17) / 30] * 100 = 43.33% decrease.
-
Finding the original value: If 17 represents 56.67% of a value, we can find the original value by using the formula: Original Value = (17 / 56.67) * 100 = 30.
-
Working with multiple percentages: Suppose a value is increased by 10% and then decreased by 5%. The final result will not be a simple addition or subtraction of percentages. Careful step-by-step calculations are needed to get the accurate final percentage.
Tips for Mastering Percentage Calculations
-
Practice regularly: Consistent practice is key to building proficiency in percentage calculations. Try solving various problems, starting with simple examples and gradually increasing complexity.
-
Understand the concept: Focus on understanding the underlying principles of percentages as proportions and fractions, rather than just memorizing formulas.
-
Utilize available tools: Employ calculators and online resources to verify your answers and explore different calculation methods.
-
Round appropriately: Pay attention to the required level of accuracy and round your answers appropriately, considering the context of the problem.
-
Check your work: Always double-check your calculations to ensure accuracy. Simple errors can lead to significant discrepancies in the final result.
Conclusion
Calculating 17 out of 30 as a percentage, resulting in 56.67%, is a fundamental skill with broad applications. Mastering percentage calculations empowers you to confidently tackle a wide range of problems in various fields, from everyday tasks to complex professional calculations. By understanding the different methods, practicing regularly, and utilizing available resources, you can confidently navigate the world of percentages and apply this knowledge to enhance your problem-solving skills. Remember that consistent practice and a solid grasp of the underlying principles are essential for achieving proficiency in this crucial mathematical skill. This detailed guide provides a comprehensive overview, but continuous practice and exploration of diverse applications will solidify your understanding and mastery of percentage calculations.
Latest Posts
Latest Posts
-
What Is The Average Iq For A 5 Year Old
Jul 12, 2025
-
How Many 12 Oz Cups In A Gallon
Jul 12, 2025
-
How Much Older Is John The Baptist Than Jesus
Jul 12, 2025
-
How Many Teaspoons In A Pound Of Sugar
Jul 12, 2025
-
How Do You Pass Level 12 On Bloxorz
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about 17 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.