18 Is What Percent Of 15
Kalali
Apr 08, 2025 · 5 min read
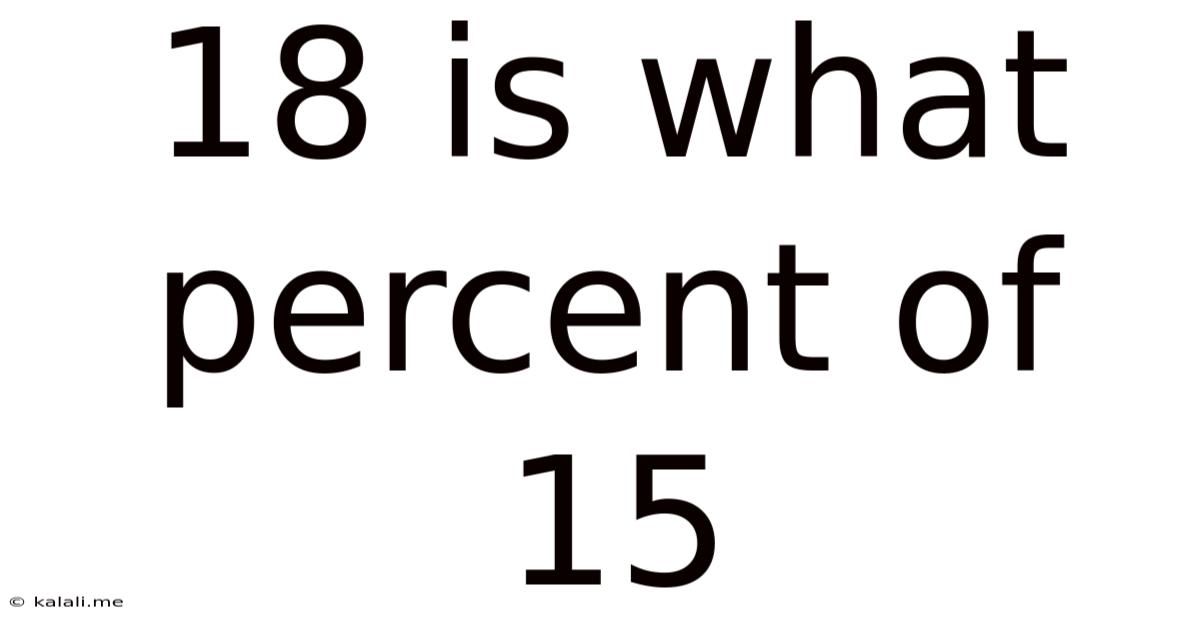
Table of Contents
18 is What Percent of 15? Understanding Percentages and Their Applications
This seemingly simple question, "18 is what percent of 15?", opens the door to a deeper understanding of percentages, their calculations, and their widespread applications in various fields. While the direct answer involves a straightforward calculation, exploring the underlying concepts provides valuable insights for anyone dealing with numerical data, from students grappling with math problems to professionals analyzing financial statements. This article will not only solve the problem but will also delve into the "why" and "how" behind percentage calculations, offering practical examples and demonstrating the importance of this fundamental concept.
Meta Description: Learn how to calculate percentages and understand the concept behind "18 is what percent of 15?". This comprehensive guide explores percentage calculations, real-world applications, and provides practical examples for various scenarios.
Understanding Percentages: A Fundamental Concept
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be easily converted into a decimal or a fraction. For instance, 50% is equivalent to 50/100, which simplifies to 1/2, or 0.5 in decimal form. This fundamental understanding is crucial for solving problems involving percentages.
Calculating "18 is What Percent of 15?"
To determine what percentage 18 represents of 15, we need to perform a simple calculation. The formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 18
- Whole: 15
Therefore, the calculation becomes:
(18 / 15) * 100% = 120%
This means that 18 is 120% of 15. This result might seem counterintuitive at first glance, as it's greater than 100%. However, this simply indicates that 18 is larger than 15.
Why the Result is Greater Than 100%
The result of 120% highlights an important aspect of percentage calculations: percentages can be greater than 100%. This occurs when the "part" is larger than the "whole." In our example, 18 is greater than 15, resulting in a percentage exceeding 100%. This simply signifies that 18 represents 120% of the value of 15.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in numerous aspects of daily life and professional fields. Here are a few examples:
-
Finance: Calculating interest rates, discounts, profits, losses, and tax rates all rely heavily on percentage calculations. Understanding percentages is essential for managing personal finances and making informed financial decisions. For example, calculating compound interest requires a solid grasp of percentage calculations.
-
Retail: Discounts and sales are often expressed as percentages. A "20% off" sale means that the price is reduced by 20% of the original price. Similarly, sales tax is added as a percentage of the purchase price.
-
Science and Statistics: Percentages are extensively used in presenting statistical data, expressing probabilities, and representing proportions within a sample or population. For instance, expressing survey results, analyzing experimental data, or reporting the prevalence of a disease often involves using percentages.
-
Education: Grades, test scores, and class performance are often expressed as percentages. Understanding percentages is crucial for students to track their academic progress and understand their performance relative to others.
-
Data Analysis: Percentages are vital in data analysis for expressing changes over time, comparing different groups, and summarizing large datasets in a concise and easily understandable manner. From market research to economic forecasting, percentages provide a standardized way to compare and interpret data.
Variations and Extensions of Percentage Problems
The fundamental concept of percentages can be extended to solve a wide array of problems. Here are a few variations:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example, if 25% of a number is 10, you can calculate the number (10 / 0.25 = 40).
-
Finding the Part: If you know the percentage and the whole, you can find the part. For example, to find 15% of 80, you would calculate 0.15 * 80 = 12.
-
Percentage Change: Calculating percentage change involves determining the increase or decrease in a value relative to its original value. This is often used to track growth or decline in various metrics. The formula is: [(New Value - Old Value) / Old Value] * 100%.
-
Percentage Increase/Decrease: These calculations are particularly useful for analyzing trends and changes over time, comparing different values, and understanding growth or decline rates.
Advanced Applications: Compound Interest and Growth Rates
Compound interest, a powerful financial tool, relies heavily on percentage calculations. It involves earning interest not only on the principal amount but also on the accumulated interest from previous periods. Understanding compound interest is crucial for making informed investment decisions and planning for long-term financial goals. Similarly, calculating growth rates in various contexts, like population growth or economic expansion, necessitates a thorough understanding of percentage calculations.
Tips for Solving Percentage Problems
-
Convert Percentages to Decimals or Fractions: This simplifies calculations and makes it easier to solve problems accurately.
-
Understand the Context: Carefully analyze the problem statement to identify the part, the whole, and the unknown quantity.
-
Use the Appropriate Formula: Select the correct formula based on what information is provided and what needs to be calculated.
-
Check Your Work: Review your calculations to ensure accuracy and identify any potential errors.
Conclusion: The Importance of Understanding Percentages
The seemingly simple question of "18 is what percent of 15?" underscores the importance of understanding percentage calculations. Percentages are an integral part of numerous aspects of daily life, from personal finance and shopping to scientific research and data analysis. Mastering percentage calculations enhances problem-solving skills and provides valuable tools for interpreting data and making informed decisions across various domains. Beyond the straightforward calculation of 120%, this article aims to equip readers with a comprehensive understanding of percentages, their applications, and their significance in a world increasingly reliant on data and numerical analysis. The ability to confidently work with percentages is a highly valuable skill that transcends academic settings and extends to nearly every facet of modern life.
Latest Posts
Latest Posts
-
4 Is What Percent Of 24
Apr 17, 2025
-
Cuanto Es 16 Grados Fahrenheit En Centigrados
Apr 17, 2025
-
How Many Meters Is 500 Feet
Apr 17, 2025
-
Is Salt Water A Heterogeneous Mixture
Apr 17, 2025
-
How Far Is A 1000 Yards
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 18 Is What Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.