18 Is What Percent Of 60
Kalali
Apr 07, 2025 · 4 min read
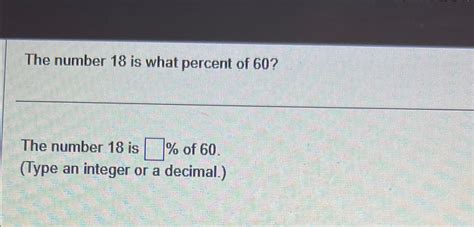
Table of Contents
18 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will not only answer the question, "18 is what percent of 60?" but will also equip you with the knowledge and tools to tackle similar percentage problems with confidence. We'll explore different methods of calculation, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 18% signifies 18 out of 100, or 18/100. This fundamental understanding is crucial for solving percentage problems.
Key Terms:
- Percentage: The portion of a whole expressed as a number out of 100.
- Base: The whole amount or total value. In our problem, 60 is the base.
- Part: The portion of the base that represents the percentage. In our problem, 18 is the part.
Method 1: Using the Percentage Formula
The most straightforward method to solve "18 is what percent of 60?" involves applying the basic percentage formula:
(Part / Base) x 100 = Percentage
Let's break down how to apply this to our problem:
-
Identify the Part and the Base: The part is 18, and the base is 60.
-
Substitute the Values: Plug these values into the formula: (18 / 60) x 100
-
Calculate the Result: First, divide 18 by 60: 18 / 60 = 0.3
-
Multiply by 100: Multiply the result by 100 to express it as a percentage: 0.3 x 100 = 30
Therefore, 18 is 30% of 60.
Method 2: Using Proportions
Another effective approach involves setting up a proportion. A proportion is a statement of equality between two ratios. We can represent our problem as:
18/60 = x/100
Where 'x' represents the unknown percentage.
To solve for 'x,' we cross-multiply:
18 * 100 = 60 * x
1800 = 60x
Now, divide both sides by 60 to isolate 'x':
x = 1800 / 60
x = 30
Again, we find that 18 is 30% of 60.
Method 3: Using Decimal Conversions
This method involves converting the fraction representing the part over the base into a decimal and then multiplying by 100 to obtain the percentage.
-
Form the Fraction: Create the fraction 18/60.
-
Convert to Decimal: Divide 18 by 60: 18 / 60 = 0.3
-
Multiply by 100: Multiply the decimal by 100 to get the percentage: 0.3 x 100 = 30%
Once again, the answer is 30%.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios. Let's explore some examples:
1. Sales and Discounts:
Imagine a store offers a 30% discount on a $60 item. To calculate the discount amount, you would use the same percentage formula:
(30/100) x $60 = $18
The discount is $18, making the final price $42. This is directly related to our original problem, demonstrating the practical application of percentage calculations.
2. Grade Calculations:
If you scored 18 out of 60 on a test, your percentage score would be 30%. This method helps to standardize grading across various tests with different point totals.
3. Financial Analysis:
Businesses utilize percentage calculations extensively to analyze financial data, such as profit margins, revenue growth, and expense ratios. Understanding percentages is crucial for interpreting financial statements and making informed decisions.
4. Data Analysis:
In many fields, including statistics and scientific research, percentages are used to represent proportions and analyze data trends. For instance, if a survey shows 18 out of 60 respondents prefer a particular product, that represents a 30% preference.
Expanding Your Knowledge: More Complex Percentage Problems
While we've focused on a simple percentage calculation, the principles discussed can be applied to more complex scenarios. Here are some examples:
- Finding the Base: If you know the percentage and the part, you can find the base using a slightly modified formula.
- Finding the Part: Similarly, if you know the percentage and the base, you can calculate the part.
- Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values and expressing it as a percentage of the original value.
Conclusion: Mastering Percentages for Success
The ability to calculate percentages accurately and efficiently is a valuable skill applicable in numerous aspects of life. By understanding the fundamental concepts, formulas, and various calculation methods, you can confidently tackle percentage problems, from simple calculations like "18 is what percent of 60?" to more complex scenarios in various fields. This comprehensive guide has provided you with the tools to master percentages and use them to analyze data, make informed decisions, and excel in various contexts. Remember to practice regularly to build your confidence and proficiency in percentage calculations. This will not only help you with everyday tasks but also enhance your analytical skills for future success.
Latest Posts
Latest Posts
-
How Many Pints In Half A Gallon
Apr 10, 2025
-
Is 16 A Prime Number Or A Composite Number
Apr 10, 2025
-
How Many Feet In 132 Inches
Apr 10, 2025
-
How Many Centimeters Is 16 Inches
Apr 10, 2025
-
What Percent Of 80 Is 15
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about 18 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.