19 Out Of 21 As A Percentage
Kalali
Apr 10, 2025 · 5 min read
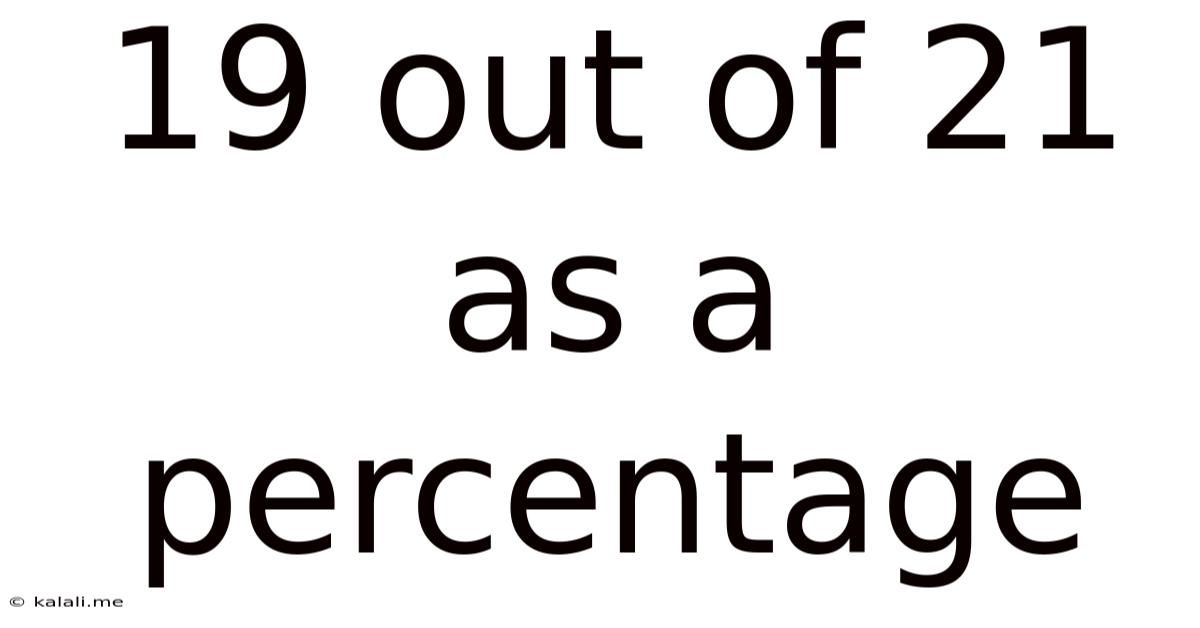
Table of Contents
19 Out of 21 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to express fractions as percentages is crucial for interpreting data, making comparisons, and communicating information effectively. This comprehensive guide delves into the calculation of 19 out of 21 as a percentage, exploring the underlying methodology and providing various approaches to solve similar problems. We'll also touch upon practical applications and explore related percentage calculations to solidify your understanding.
What Does 19 Out of 21 Mean?
The phrase "19 out of 21" represents a fraction, specifically 19/21. This fraction indicates that 19 represents a portion of a larger whole, which in this case is 21. To express this fraction as a percentage, we need to convert it to a form that represents a proportion out of 100. This is where percentage calculations come into play. Understanding this fundamental concept is the first step towards mastering percentage conversions. This is particularly useful when comparing results, understanding ratios, or presenting data in a more digestible format.
Method 1: Using the Basic Percentage Formula
The most straightforward method to calculate 19 out of 21 as a percentage involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this scenario:
- Part: 19
- Whole: 21
Substituting these values into the formula:
(19 / 21) * 100% = 90.476% (approximately)
Therefore, 19 out of 21 is approximately 90.48%. Rounding to two decimal places is standard practice for most applications. The precision required might vary depending on the context; for instance, a scientific study might demand greater accuracy than a simple sales report.
Method 2: Converting the Fraction to a Decimal
An alternative approach involves first converting the fraction 19/21 to a decimal and then multiplying by 100% to obtain the percentage.
To convert 19/21 to a decimal, we perform the division:
19 ÷ 21 ≈ 0.90476
Now, multiply the decimal by 100%:
0.90476 * 100% ≈ 90.48%
This method yields the same result as the previous one, demonstrating the equivalence of the two approaches. The choice between these methods often comes down to personal preference and the tools available; a calculator is highly beneficial for both methods, especially when dealing with more complex fractions.
Method 3: Using Proportions
Another way to approach this problem is by setting up a proportion. We can express the problem as:
19/21 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
21x = 1900
x = 1900 / 21 ≈ 90.48%
This method reinforces the concept of proportional reasoning and offers a different perspective on the percentage calculation. It’s particularly useful when explaining the concept to students or those new to percentage calculations. This method visually demonstrates the relationship between the fraction and the equivalent percentage.
Understanding the Result: 90.48%
The result, approximately 90.48%, signifies that 19 represents 90.48% of 21. This information is valuable for comparing proportions, interpreting data, and making informed decisions in various scenarios. For example, if 21 represents the total number of students in a class and 19 of them passed an exam, then the pass rate is approximately 90.48%.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in numerous real-world scenarios. Here are a few examples:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve percentage calculations. Understanding percentage change is crucial for tracking investment performance.
- Statistics: Percentages are fundamental in expressing probabilities, frequencies, and proportions within datasets. Analyzing survey results or demographic data often involves extensive use of percentages.
- Science: Many scientific calculations and measurements rely on percentages, such as calculating concentrations, error rates, and experimental yields.
- Retail: Sales, discounts, and markups are all expressed as percentages, making them crucial for pricing strategies and consumer understanding.
- Education: Grade calculations, test scores, and performance metrics are typically expressed as percentages.
Related Percentage Calculations
To further enhance your understanding of percentage calculations, let's explore some related examples:
-
Calculating the percentage of something remaining: If 19 out of 21 items are sold, what percentage remains unsold? This involves calculating (21 - 19) / 21 * 100% = 9.52%.
-
Calculating percentage increase or decrease: If the number of items increased from 19 to 21, the percentage increase would be calculated as (21 - 19) / 19 * 100% = 10.53%. Conversely, a decrease from 21 to 19 represents a percentage decrease of (21 - 19) / 21 * 100% = 9.52%.
-
Dealing with larger numbers: The same principles apply when dealing with larger numbers. For example, calculating 1900 out of 2100 as a percentage would yield the same result (approximately 90.48%). The size of the numbers doesn't change the fundamental method.
-
Percentage points vs. percentages: It's important to distinguish between percentage points and percentages. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the original 20%. This distinction is crucial for accurate interpretation and reporting.
Tips for Accurate Percentage Calculations
-
Use a calculator: Calculators are invaluable for accurate and efficient percentage calculations, especially with complex fractions or larger numbers.
-
Round appropriately: Round your final answer to an appropriate number of decimal places based on the context. Avoid unnecessary precision.
-
Double-check your work: Always double-check your calculations to ensure accuracy. Simple errors can lead to significant discrepancies.
-
Understand the context: Always consider the context of the problem to interpret the results correctly and draw meaningful conclusions.
Conclusion
Calculating 19 out of 21 as a percentage is a straightforward process involving the application of the basic percentage formula or alternative methods. Understanding percentage calculations is essential across various disciplines and day-to-day activities. By mastering the techniques outlined in this guide, you'll enhance your ability to interpret data, make informed decisions, and communicate information effectively. Remember to practice regularly, explore different methods, and always double-check your work to ensure accuracy. The ability to confidently perform percentage calculations is a valuable skill that will serve you well in numerous aspects of life.
Latest Posts
Latest Posts
-
Who Did Alan Jackson Have An Affair With
Jul 04, 2025
-
How Much Is 500 Grams Of Ground Beef
Jul 04, 2025
-
1 Pound Pasta Is How Many Cups
Jul 04, 2025
-
How Many Cans Of Soda Are In A 2 Liter
Jul 04, 2025
-
How Do U Say Of In Spanish
Jul 04, 2025
Related Post
Thank you for visiting our website which covers about 19 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.