19 Out Of 25 As A Percentage
Kalali
Mar 06, 2025 · 5 min read
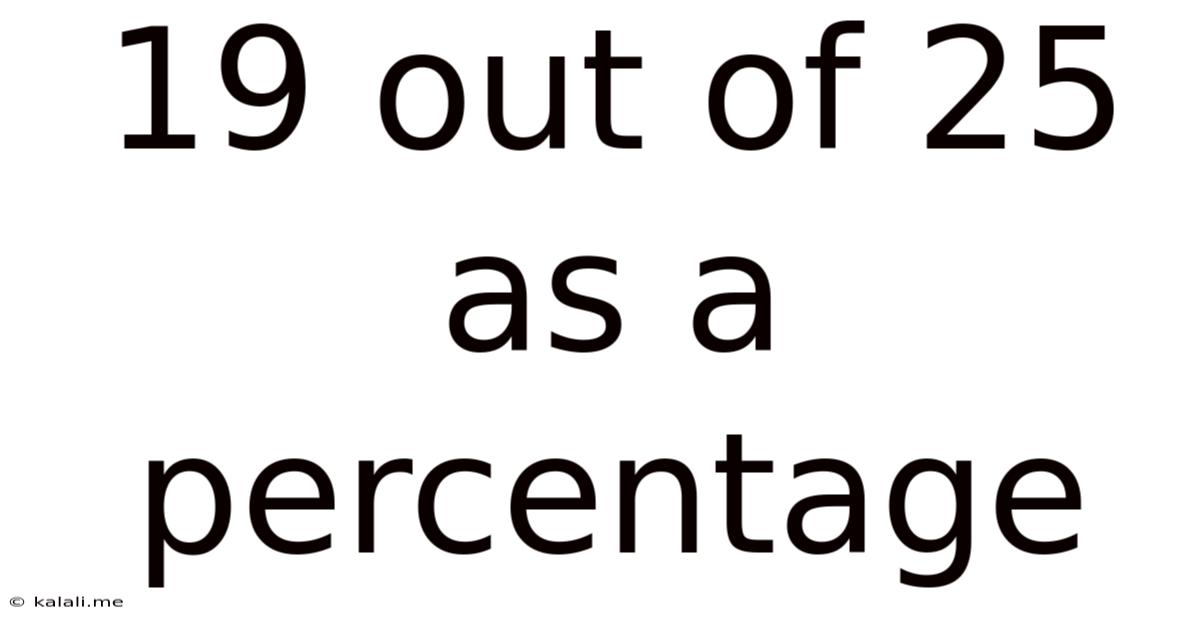
Table of Contents
19 out of 25 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with broad applications across various fields, from academic assessments to financial analysis and everyday life scenarios. Understanding how to convert fractions into percentages allows you to quickly interpret data, make informed decisions, and communicate numerical information effectively. This article delves into the specific calculation of 19 out of 25 as a percentage, providing a step-by-step guide and exploring various related concepts to solidify your understanding.
Understanding Percentages
Before we dive into the specific calculation, let's refresh our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Percentages are widely used because they offer a standardized and easily comparable way to represent proportions.
For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Similarly, 25% means 25 out of 100, or 25/100, simplifying to 1/4. Understanding this fundamental relationship is crucial for converting fractions to percentages.
Calculating 19 out of 25 as a Percentage: The Step-by-Step Method
To calculate 19 out of 25 as a percentage, we follow these simple steps:
Step 1: Express the Fraction
First, represent the given information as a fraction. "19 out of 25" translates to the fraction 19/25.
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number). In this case:
19 ÷ 25 = 0.76
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.76 x 100 = 76%
Therefore, 19 out of 25 is equal to 76%.
Alternative Calculation Methods
While the above method is straightforward, there are alternative approaches you can use, depending on your comfort level with mathematical operations.
Method 2: Using Proportions
You can solve this problem using proportions. We know that a percentage is a fraction of 100. We can set up a proportion:
19/25 = x/100
To solve for x (the percentage), we cross-multiply:
25x = 1900
x = 1900/25
x = 76
Therefore, x = 76%, confirming our previous result.
Method 3: Mental Calculation (Approximation)
For quick estimations, you can utilize mental math. Since 25 is a quarter of 100, you can think of 19 out of 25 as approximately 19 quarters. Four quarters make a whole, meaning 20 quarters would be 80%. Since 19 is one quarter less than 20, a close approximation is 80% - 4% = 76%. This approach helps in quickly estimating percentages, particularly in situations where precision isn't paramount.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential across a range of scenarios:
-
Academic Performance: Calculating your grade in a class often involves converting the number of correct answers to a percentage of the total possible points. A score of 19 out of 25 on a test, as we've demonstrated, results in a 76% grade.
-
Financial Matters: Percentages are ubiquitous in finance. Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely on percentage calculations. For example, understanding a 76% discount on an item offers a substantial savings opportunity.
-
Data Analysis and Interpretation: In many fields, data is presented as percentages to simplify the interpretation of complex datasets. Understanding percentage changes allows for better comprehension of trends and patterns. A 76% increase in sales, for example, represents significant growth.
-
Everyday Life: Percentage calculations are relevant in various everyday situations. Calculating tips in restaurants, understanding sales discounts in stores, or determining the percentage of a task completed all rely on this fundamental skill.
Advanced Percentage Calculations and Related Concepts
Beyond the basic calculations, several advanced concepts build upon the foundation of percentages:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] x 100. For percentage decrease, the formula is: [(Old Value - New Value) / Old Value] x 100.
-
Percentage Points: It's crucial to differentiate between percentage points and percentage change. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase in the actual value.
-
Compounding Percentages: This refers to situations where percentages are applied repeatedly, such as compound interest. The formula for compound interest takes into account both the principal amount and the accumulated interest over time.
-
Weighted Averages: Weighted averages consider the relative importance of different values when calculating the average. For example, calculating a final grade that considers different assignment weights uses a weighted average.
Common Mistakes to Avoid When Calculating Percentages
Several common errors can lead to incorrect percentage calculations. Being aware of these pitfalls helps ensure accuracy:
-
Incorrect Fraction Formation: Ensure that the fraction representing "x out of y" is properly set up, with 'x' as the numerator and 'y' as the denominator.
-
Improper Decimal-to-Percentage Conversion: Always remember to multiply the decimal by 100 when converting to a percentage and add the % symbol.
-
Confusion Between Percentage Points and Percentage Change: Clearly understand the difference between these two concepts to avoid misinterpretations.
-
Rounding Errors: Rounding off numbers prematurely during calculations can lead to inaccuracies in the final result. Aim to round only at the final stage of calculation.
Conclusion: Mastering Percentage Calculations for Success
The ability to calculate percentages is a vital life skill, applicable in numerous professional and personal contexts. Understanding the different methods, applications, and potential pitfalls associated with percentage calculations provides a solid foundation for effective data interpretation and decision-making. Whether you're assessing academic performance, navigating financial matters, or interpreting data in your chosen field, mastering percentage calculations equips you with a powerful tool for success. The simple calculation of 19 out of 25 as 76%, as demonstrated in this article, serves as a stepping stone to a deeper understanding of this fundamental concept and its wide-ranging applications. Remember to practice regularly and refine your approach to ensure accuracy and proficiency in percentage calculations.
Latest Posts
Latest Posts
-
What Do You Get When You Phone A Bee
Jul 04, 2025
-
Was Jennifer Aniston In Sex And The City
Jul 04, 2025
-
Is Dried Oregano A Pure Substance Or Mixture
Jul 04, 2025
-
What Is Fgteev Duddys Real Phone Number
Jul 04, 2025
-
What Are 2004 Pennies Worth Worlds Easyest Game
Jul 04, 2025
Related Post
Thank you for visiting our website which covers about 19 Out Of 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.