19 Out Of 30 As A Percentage
Kalali
Mar 10, 2025 · 5 min read
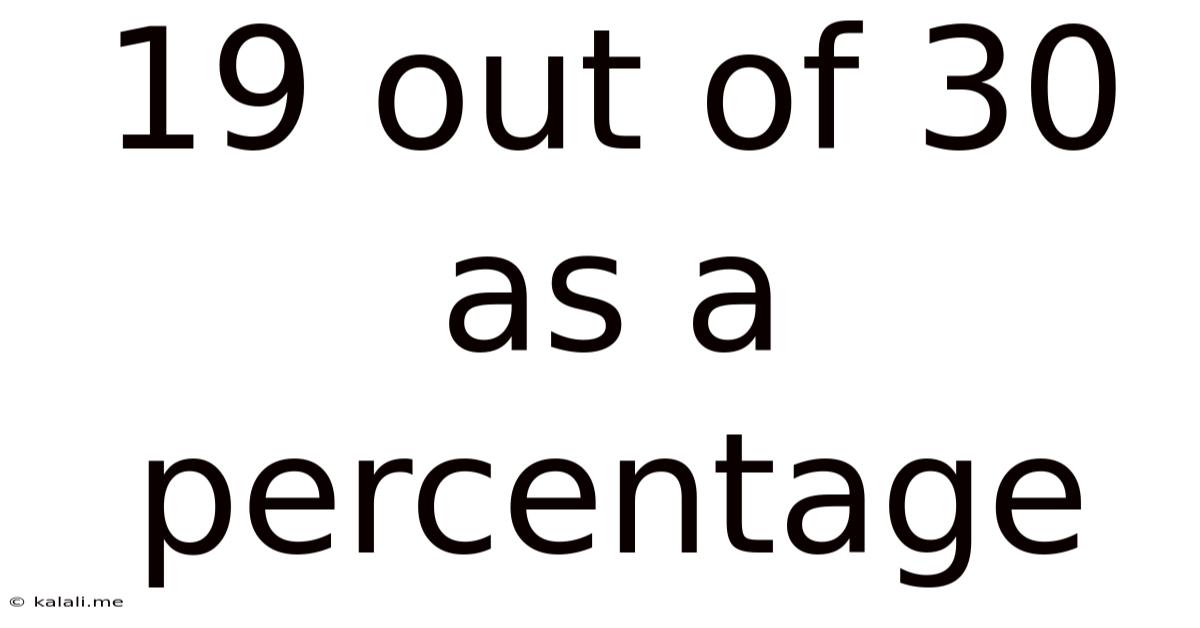
Table of Contents
19 out of 30 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with broad applications in various fields. Understanding this process is crucial for interpreting data, making comparisons, and communicating information effectively. This article delves deep into calculating "19 out of 30 as a percentage," exploring the methodology, providing practical examples, and discussing its relevance in different contexts. We'll also cover related percentage calculations and offer tips for improving your understanding of percentages in general.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the specific calculation, let's refresh our understanding of the fundamental relationships between fractions, decimals, and percentages.
-
Fractions: Represent parts of a whole. In our case, "19 out of 30" is a fraction, written as 19/30. The numerator (19) represents the part, and the denominator (30) represents the whole.
-
Decimals: Represent fractions in base-10 notation. To convert a fraction to a decimal, we divide the numerator by the denominator. For example, 19/30 = 0.6333... (the 3s repeat infinitely).
-
Percentages: Represent a fraction or decimal as a portion of 100. The percentage symbol (%) means "out of 100" or "per hundred."
The core concept is that these three representations are interchangeable; each can be converted to the other two.
Calculating 19 out of 30 as a Percentage: Step-by-Step
To express 19 out of 30 as a percentage, we follow these steps:
Step 1: Convert the fraction to a decimal:
Divide the numerator (19) by the denominator (30):
19 ÷ 30 ≈ 0.6333
Step 2: Convert the decimal to a percentage:
Multiply the decimal by 100 and add the percentage symbol (%):
0.6333 × 100 ≈ 63.33%
Therefore, 19 out of 30 is approximately 63.33%. The use of "approximately" is important here because the decimal representation of 19/30 is a repeating decimal. For most practical purposes, rounding to two decimal places (63.33%) is sufficient.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios. Here are a few examples:
-
Academic Performance: If a student answers 19 questions correctly out of 30 on a test, their score is 63.33%. This allows for easy comparison of student performance.
-
Sales and Discounts: A store offering a 63.33% discount on an item means the customer pays only 36.67% of the original price. This is a practical application of subtracting a percentage from a whole.
-
Financial Analysis: In investment, a 63.33% return on investment (ROI) indicates a significant profit. Percentages are essential for evaluating financial performance.
-
Statistical Analysis: In surveys and polls, percentages are used to represent the proportion of respondents who hold a particular view. For example, if 19 out of 30 respondents favored a certain candidate, their support is 63.33%.
-
Scientific Research: Percentages are frequently used to report experimental results, such as the success rate of a treatment or the percentage of a population exhibiting a specific characteristic.
Variations and Related Percentage Calculations
Let's explore some related percentage calculations that build upon the understanding of 19/30:
1. Calculating the remaining percentage: If 19 out of 30 represents a certain portion, the remaining percentage is 100% - 63.33% = 36.67%. This highlights the complementary nature of percentages.
2. Scaling up: What if there were 60 questions instead of 30, and the same proportion of correct answers was maintained? We would expect 2 × 19 = 38 correct answers. This demonstrates how percentages can be used to scale proportions.
3. Comparing percentages: Suppose another student scored 22 out of 30. That's (22/30) × 100 ≈ 73.33%. By comparing percentages (63.33% vs 73.33%), we can readily compare the relative performance of the two students.
Improving Your Understanding of Percentages
Mastering percentages requires practice and a solid understanding of the underlying principles. Here are some tips:
-
Practice regularly: Solve various percentage problems to build your skills and confidence. Start with simple problems and gradually increase the complexity.
-
Use online resources: Numerous websites and apps offer interactive exercises and tutorials on percentage calculations.
-
Visual aids: Charts and graphs can help visualize percentages and make them easier to understand.
-
Real-world application: Look for opportunities to apply percentage calculations in your daily life, such as calculating discounts, tips, or taxes.
Advanced Concepts and Applications
Beyond the basic calculations, several advanced concepts related to percentages exist:
-
Compounding percentages: This refers to applying percentages successively, commonly seen in interest calculations where interest is added to the principal, and future interest is calculated on the increased amount.
-
Percentage change: Calculating the percentage increase or decrease between two values is a valuable skill in trend analysis and comparative studies.
-
Weighted averages: These involve assigning different weights or importance to different values before calculating the average, often expressed as a percentage.
Conclusion: The Importance of Percentage Calculations in Daily Life
This in-depth exploration of "19 out of 30 as a percentage" reveals its practical significance and the importance of understanding percentage calculations. From simple everyday tasks to complex financial and scientific applications, the ability to convert fractions and decimals to percentages and work fluently with percentages is a cornerstone of numerical literacy. By consistently practicing and applying the concepts discussed, you will enhance your mathematical proficiency and gain a valuable skill applicable across diverse areas of life. Remember that consistent practice and understanding the underlying principles are key to mastering percentage calculations and applying them confidently in various situations. The ability to quickly and accurately calculate percentages will undoubtedly enhance your problem-solving skills and improve your analytical capabilities.
Latest Posts
Latest Posts
-
What Is The Average Iq For A 5 Year Old
Jul 12, 2025
-
How Many 12 Oz Cups In A Gallon
Jul 12, 2025
-
How Much Older Is John The Baptist Than Jesus
Jul 12, 2025
-
How Many Teaspoons In A Pound Of Sugar
Jul 12, 2025
-
How Do You Pass Level 12 On Bloxorz
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about 19 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.