2 1 4 In Decimal Form
Kalali
Mar 24, 2025 · 6 min read
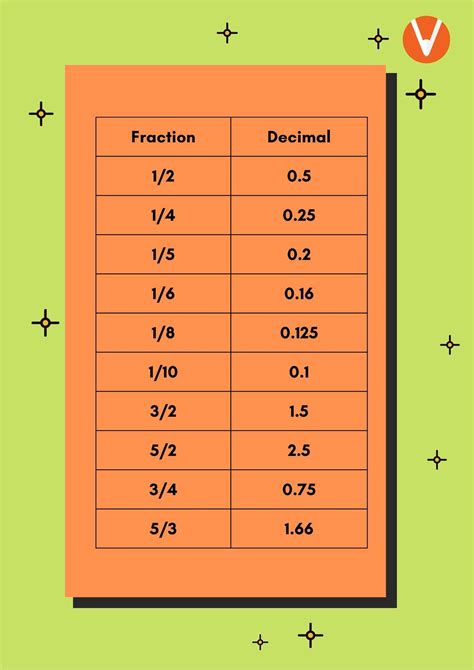
Table of Contents
2 1/4 in Decimal Form: A Comprehensive Guide
The seemingly simple question, "What is 2 1/4 in decimal form?", opens a door to a deeper understanding of fractions, decimals, and their interconnectedness within the broader world of mathematics. This comprehensive guide will explore not only the answer but also the underlying principles, practical applications, and various methods for converting mixed numbers like 2 1/4 into their decimal equivalents. We'll delve into the reasons behind these conversions and demonstrate their relevance in various fields.
Understanding Fractions and Decimals
Before diving into the conversion of 2 1/4, let's establish a solid foundation by understanding the fundamental concepts of fractions and decimals.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) represents that the whole is divided into four equal parts.
Decimals: Another Way to Express Parts of a Whole
Decimals are another way to express parts of a whole. They use a base-ten system, where each digit to the right of the decimal point represents a power of ten. The first digit after the decimal point represents tenths (1/10), the second represents hundredths (1/100), the third represents thousandths (1/1000), and so on. For example, 0.25 represents 2 tenths and 5 hundredths, or 25/100.
Mixed Numbers: Combining Whole Numbers and Fractions
A mixed number combines a whole number and a fraction. For example, 2 1/4 represents two whole units plus one-quarter of another unit. Converting mixed numbers to decimals involves converting the fractional part to its decimal equivalent and then adding it to the whole number.
Converting 2 1/4 to Decimal Form: The Methods
There are several methods to convert 2 1/4 to its decimal form. Let's explore the most common and straightforward approaches.
Method 1: Converting the Fraction to a Decimal
This method involves first converting the fraction 1/4 into its decimal equivalent and then adding it to the whole number 2.
- Divide the numerator by the denominator: Divide 1 by 4. This gives you 0.25.
- Add the whole number: Add the result (0.25) to the whole number (2). This yields 2.25.
Therefore, 2 1/4 in decimal form is 2.25.
Method 2: Converting the Mixed Number to an Improper Fraction
This method involves first converting the mixed number 2 1/4 into an improper fraction, and then converting the improper fraction to a decimal.
- Convert to an improper fraction: To convert 2 1/4 to an improper fraction, multiply the whole number (2) by the denominator (4), add the numerator (1), and keep the same denominator (4). This results in (2 * 4 + 1)/4 = 9/4.
- Divide the numerator by the denominator: Divide 9 by 4. This gives you 2.25.
Again, the decimal equivalent of 2 1/4 is 2.25.
Method 3: Using a Calculator
The simplest method is to use a calculator. Enter "2 + 1 ÷ 4" or "9 ÷ 4" into your calculator. The result will be 2.25.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is crucial in various real-world applications across numerous disciplines. Let's explore a few:
Finance and Accounting
In finance, dealing with monetary values necessitates accurate decimal representation. Calculating interest rates, discounts, or profit margins often involves converting fractions to decimals for ease of calculation and understanding. For instance, a discount of 1/4 or 25% is easily represented as 0.25 for quick calculations.
Measurement and Engineering
In engineering and other fields involving precise measurements, converting fractions to decimals is essential for accuracy. Dimensions of components, material quantities, and other specifications are often expressed in decimal form for streamlined calculations and consistency. Imagine designing a circuit board; precise decimal measurements are crucial for proper functionality.
Data Analysis and Statistics
In data analysis and statistics, converting fractions to decimals is common practice. Data sets often include fractional values, which need to be converted to decimals for computation and analysis using statistical software and tools. This helps in performing calculations like averages, standard deviations, and other statistical measures.
Cooking and Baking
Even in cooking and baking, converting fractions to decimals can be helpful. Recipes often use fractional measurements for ingredients. Converting these fractions to decimals allows for easier scaling of recipes or using measuring tools calibrated in decimal units.
Programming and Computer Science
In programming, representing fractional values often requires decimal representation. Many programming languages use floating-point numbers (which are essentially decimals) to store and manipulate fractional data. Converting fractions to decimals ensures accurate and efficient data processing within computer programs.
Beyond 2 1/4: Expanding the Concept
While this guide focuses on 2 1/4, the principles of fraction-to-decimal conversion apply to any fraction or mixed number. Understanding the underlying concepts allows you to confidently convert any fraction into its decimal equivalent. This skill is fundamental to numerous mathematical operations and real-world applications.
Advanced Concepts and Considerations
This section will delve into some more advanced aspects related to decimal conversions, broadening the scope of understanding beyond the basic conversion of 2 1/4.
Recurring Decimals
Not all fractions translate into neat, terminating decimals like 2.25. Some fractions result in recurring decimals, where a sequence of digits repeats infinitely. For instance, 1/3 translates to 0.3333... Understanding how to represent and work with recurring decimals is essential in more advanced mathematical contexts.
Significant Figures and Rounding
When working with decimals, especially those obtained from conversions involving approximations or measurements, it's crucial to understand significant figures and rounding. This ensures that the final decimal representation maintains the appropriate level of accuracy and precision relative to the original data.
Using Different Bases
The decimal system (base-10) is not the only number system used. Other number systems, such as binary (base-2), hexadecimal (base-16), and octal (base-8), are also employed, particularly in computer science and related fields. Converting fractions to decimals in these different bases involves different mathematical procedures and interpretations.
Conclusion: Mastering Decimal Conversions
Converting fractions to decimals, as exemplified by the conversion of 2 1/4 to 2.25, is a fundamental skill with broad applications. Understanding the various methods, their underlying principles, and their practical implications empowers individuals to handle numerical data with greater confidence and accuracy across various disciplines. From finance and engineering to cooking and programming, the ability to fluently convert between fractions and decimals is indispensable for success. By mastering this concept, you pave the way for more complex mathematical explorations and enhance your problem-solving capabilities in numerous real-world scenarios. Remember to practice regularly and explore different methods to solidify your understanding and improve your proficiency in decimal conversions.
Latest Posts
Latest Posts
-
15 Ml Is How Many Ounces
Mar 29, 2025
-
How Many Feet Is 66 In
Mar 29, 2025
-
108 Cm Is How Many Inches
Mar 29, 2025
-
180 Cm Is How Many Feet
Mar 29, 2025
-
How Many Feet In 32 Inches
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about 2 1 4 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
