2 Is What Percent Of 1000
Kalali
Apr 12, 2025 · 5 min read
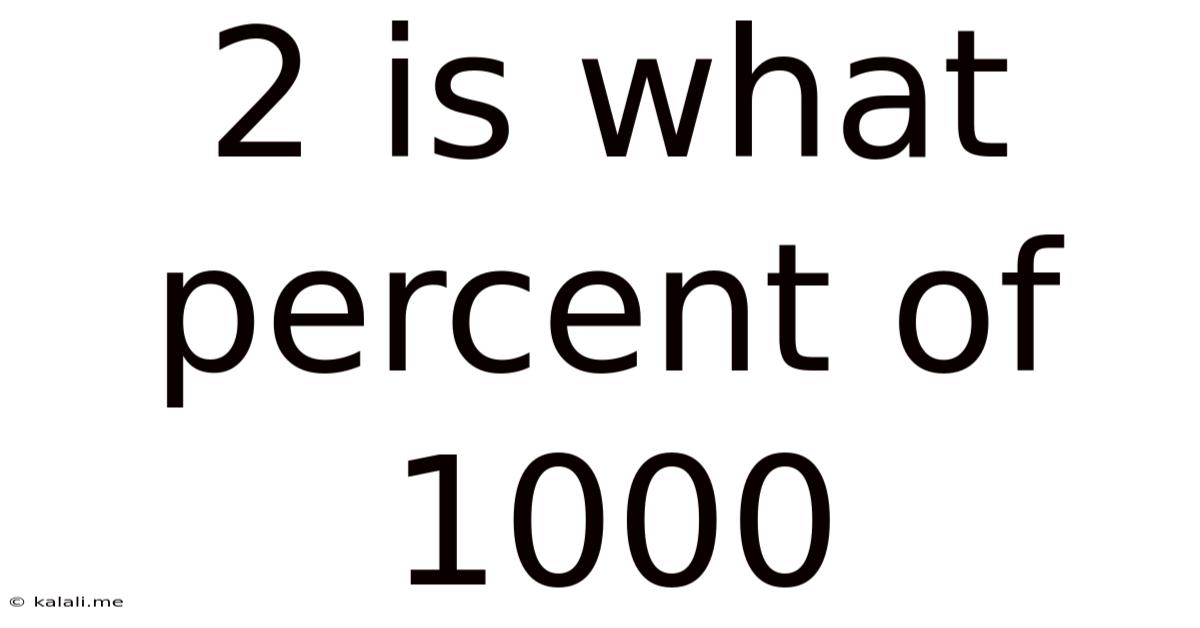
Table of Contents
2 is What Percent of 1000? A Deep Dive into Percentage Calculations
This seemingly simple question, "2 is what percent of 1000?", opens the door to a broader understanding of percentages, their applications, and how to solve percentage problems efficiently. While the answer might seem immediately obvious to some, understanding the underlying principles is crucial for tackling more complex percentage calculations encountered in various fields, from finance and statistics to everyday life. This article will not only provide the answer but also explore the methodology, variations, and practical applications of percentage calculations.
Meta Description: Discover how to calculate percentages with a detailed explanation of how to determine what percent 2 is of 1000. This comprehensive guide covers the basic formula, practical applications, and explores more complex percentage problems.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this fundamental concept is key to solving any percentage problem.
Calculating "2 is What Percent of 1000?"
The core formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 2
- Whole: 1000
Plugging these values into the formula:
(2 / 1000) * 100% = 0.2%
Therefore, 2 is 0.2% of 1000.
Different Approaches to Solving Percentage Problems
While the above method is straightforward, there are alternative approaches that can be useful depending on the complexity of the problem. Let's explore a few:
-
Using Proportions: This method sets up a proportion to solve for the unknown percentage. The proportion would be:
2/1000 = x/100
Solving for x (the percentage):
x = (2 * 100) / 1000 = 0.2%
-
Using Decimal Conversion: First, divide the part by the whole: 2 / 1000 = 0.002. Then, multiply the result by 100 to express it as a percentage: 0.002 * 100% = 0.2%. This method is particularly efficient when working with calculators.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and returns on investment (ROI) all rely heavily on percentage calculations. For instance, calculating the interest accrued on a loan or the discount on a sale item requires a clear understanding of percentages. Understanding compound interest, which involves applying percentages repeatedly over time, is crucial for long-term financial planning.
-
Statistics: Percentages are fundamental in statistical analysis. They are used to represent proportions, probabilities, and changes in data. For example, expressing survey results, analyzing population demographics, or calculating the success rate of a medical treatment often involves percentage calculations. Confidence intervals and hypothesis testing also utilize percentages extensively.
-
Science: Percentage calculations are ubiquitous in scientific research. Expressing concentrations of solutions, measuring error margins in experiments, and analyzing the composition of substances all involve calculating and interpreting percentages. For instance, determining the percentage of a particular element in a compound or the percentage change in a physical quantity during an experiment uses percentage calculations.
-
Everyday Life: Percentages are encountered daily, from calculating tips at restaurants to understanding sale prices in stores. Analyzing nutritional information on food labels, understanding the percentage of a discount offered on a product, or even interpreting weather forecasts (e.g., a 30% chance of rain) requires a basic understanding of percentages.
Beyond the Basics: More Complex Percentage Problems
While "2 is what percent of 1000?" is a relatively simple problem, let's explore some more challenging scenarios that build on the fundamental principles:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example, if 10% of a number is 20, what is the number? The formula can be rearranged to: Whole = (Part / Percentage) * 100.
-
Finding the Part: If you know the percentage and the whole, you can calculate the part. For example, what is 15% of 500? The formula can be adapted to: Part = (Percentage / 100) * Whole.
-
Percentage Increase/Decrease: These calculations determine the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100%. The formula for percentage decrease is similar, but the difference is subtracted from the old value. These are crucial in analyzing trends and growth in various fields.
-
Compound Percentage Changes: This involves applying a percentage change multiple times, which is frequently used in finance to calculate compound interest. Each time a percentage is applied, the new value becomes the basis for the next calculation.
-
Percentage Points vs. Percentages: It's important to distinguish between percentage points and percentages. A change from 10% to 20% is a 10 percentage point increase, but a 100% increase in percentage terms. This distinction is often crucial in financial reporting and statistical analysis.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The best way to master percentage calculations is to practice regularly with different types of problems. Start with simple problems and gradually increase the complexity.
-
Use Calculators Strategically: While mental calculations can be helpful for simple problems, using a calculator efficiently can save time and prevent errors, particularly for complex percentage calculations.
-
Understand the Formula Thoroughly: Memorizing the basic formula and understanding how to rearrange it for different scenarios is crucial.
-
Break Down Complex Problems: For complex problems, break them down into smaller, manageable steps. This will make the calculation process easier and less prone to errors.
-
Check Your Work: Always check your answers to ensure accuracy. A simple way to do this is to work backward from your answer to see if you arrive at the original values.
Conclusion
Understanding how to calculate percentages is a fundamental skill with broad applications across numerous disciplines. The seemingly simple question, "2 is what percent of 1000?", serves as a gateway to exploring a world of percentage calculations, from basic to complex scenarios. By mastering the core principles, formulas, and various approaches outlined in this article, you can confidently tackle any percentage problem and apply this knowledge effectively in your personal and professional life. Remember to practice regularly and utilize the tips and tricks provided to enhance your skills and achieve accuracy. The ability to calculate and interpret percentages is a valuable tool that will benefit you in countless ways.
Latest Posts
Latest Posts
-
Born In 1990 How Old Am I
Jul 12, 2025
-
What Is The Average Iq For A 5 Year Old
Jul 12, 2025
-
How Many 12 Oz Cups In A Gallon
Jul 12, 2025
-
How Much Older Is John The Baptist Than Jesus
Jul 12, 2025
-
How Many Teaspoons In A Pound Of Sugar
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.