2 Is What Percent Of 6
Kalali
Apr 17, 2025 · 5 min read
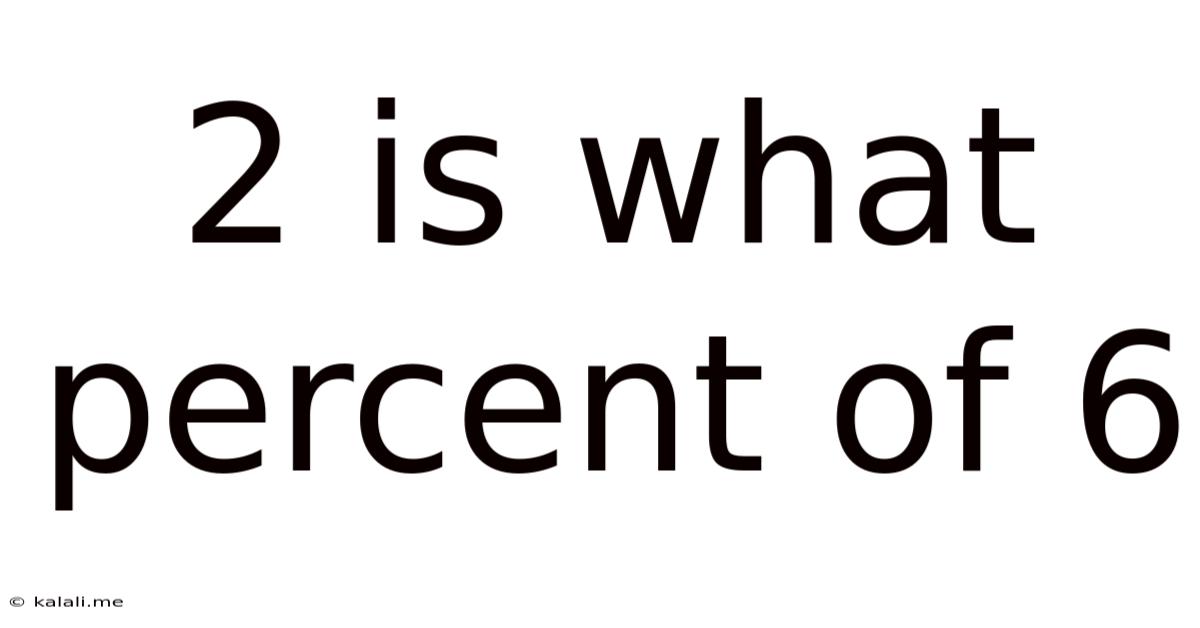
Table of Contents
2 is What Percent of 6? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "2 is what percent of 6?", opens the door to a fascinating world of percentages, their calculations, and their wide-ranging applications in everyday life and various fields. Understanding percentages is fundamental to interpreting data, making financial decisions, and comprehending information presented in various formats. This article will not only answer the initial question but also explore the underlying concepts, provide multiple methods for solving similar problems, and showcase real-world examples where this type of calculation is essential.
Meta Description: Discover how to calculate percentages, understand the concept of "2 is what percent of 6," and explore its real-world applications in finance, statistics, and more. Learn multiple calculation methods and master percentage problems.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are a convenient way to represent proportions and changes in quantities. They offer a standardized way to compare different values regardless of their initial magnitudes. For example, a 10% increase in sales is easily understood and comparable across different product lines or businesses, even if the absolute sales figures vary significantly.
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our example, "2 is what percent of 6?", 2 is the "part," and 6 is the "whole." Applying the formula, we get:
(2 / 6) * 100% = 33.33% (approximately)
Multiple Methods for Calculating Percentages
While the basic formula is straightforward, there are several approaches to calculate percentages, each with its own advantages depending on the context and your comfort level with mathematical operations:
Method 1: Using the Basic Formula (as shown above)
This is the most direct and widely understood method. It involves substituting the values into the formula and performing the calculations. This method is ideal for simple percentage calculations and is easily grasped by beginners.
Method 2: Using Proportions
This method uses the concept of equivalent ratios. We can set up a proportion:
2/6 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
6x = 200
x = 200/6 = 33.33% (approximately)
This method is particularly useful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
2/6 = 0.3333...
0.3333... * 100% = 33.33% (approximately)
This approach is efficient and suitable for calculations involving decimals or when using a calculator.
Method 4: Using a Calculator
Most calculators have a percentage function (%) that simplifies the process. Simply enter "2 ÷ 6 = %" to obtain the result directly. This is the fastest and most convenient method for routine percentage calculations.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life:
1. Finance:
- Interest Rates: Calculating simple and compound interest relies heavily on percentage calculations. Understanding interest rates is crucial for making informed decisions about loans, savings accounts, and investments.
- Discounts and Sales Tax: Determining the final price of an item after applying discounts or adding sales tax involves percentage calculations.
- Profit Margins: Businesses use percentages to calculate profit margins, which represent the profitability of their products or services.
- Investment Returns: Tracking the performance of investments and calculating returns often requires percentage calculations.
2. Statistics and Data Analysis:
- Data Representation: Percentages are used extensively in charts, graphs, and tables to represent proportions of data. For example, pie charts use percentages to show the distribution of different categories within a dataset.
- Probability and Odds: Percentages are frequently used to express probabilities and odds in various scenarios.
- Survey Results: Percentages are a common way to present survey results, making it easier to understand the distribution of opinions or preferences.
3. Everyday Life:
- Tip Calculations: Calculating the appropriate tip in a restaurant involves determining a percentage of the total bill.
- Grading Systems: Many educational systems use percentages to represent student grades, providing a standardized measure of academic performance.
- Nutritional Information: Food labels often display nutritional information as percentages of recommended daily values.
- Sales and Promotions: Understanding discounts and promotional offers frequently requires calculating percentages.
Beyond the Basics: Understanding Percentage Change and Percentage Increase/Decrease
While the initial problem focuses on finding a percentage of a whole, it's important to understand related concepts like percentage change, percentage increase, and percentage decrease.
Percentage Change: This measures the relative change between an old value and a new value. The formula is:
[(New Value - Old Value) / Old Value] * 100%
Percentage Increase: This is a specific type of percentage change where the new value is greater than the old value. The calculation is the same as the percentage change formula but will always result in a positive value.
Percentage Decrease: This is a specific type of percentage change where the new value is less than the old value. The calculation is the same as the percentage change formula but will always result in a negative value.
These concepts are crucial for analyzing trends, understanding growth or decline in various metrics, and making data-driven decisions. For instance, understanding percentage increase in sales year-over-year allows businesses to evaluate their growth trajectory and make informed decisions about future strategies.
Conclusion: Mastering Percentages for Real-World Success
The question, "2 is what percent of 6?", serves as a gateway to understanding the broader world of percentages and their applications. While the calculation itself is relatively simple, the underlying concepts and their practical implications are far-reaching. By mastering the various methods of calculating percentages and understanding their role in finance, statistics, and everyday life, individuals and businesses can make informed decisions, interpret data effectively, and navigate various situations with greater confidence. The ability to swiftly and accurately perform percentage calculations is a valuable skill applicable across a multitude of contexts, proving its importance in both personal and professional spheres. From simple budgeting to complex financial modeling, the understanding of percentages is a cornerstone of numerical literacy.
Latest Posts
Latest Posts
-
What Is The Prefix Of In
Apr 19, 2025
-
The Ability Of A Substance To Catch Fire Or Burn
Apr 19, 2025
-
35 8 As A Mixed Number
Apr 19, 2025
-
What Is The Domain Of The Function Graphed Below
Apr 19, 2025
-
What Is 6 Ft 1 In Cm
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.