2 Is What Percent Of 8
Kalali
Mar 14, 2025 · 5 min read
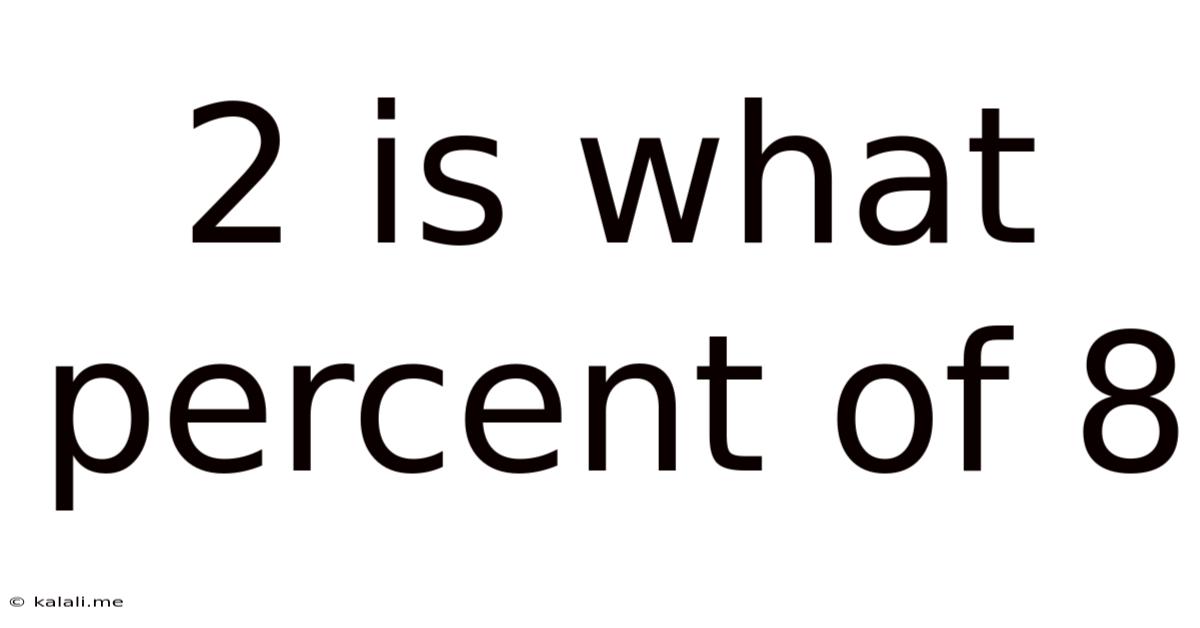
Table of Contents
2 is What Percent of 8? A Deep Dive into Percentage Calculations
This seemingly simple question, "2 is what percent of 8?", opens the door to a broader understanding of percentages, their applications, and how to solve percentage problems efficiently. While the answer might seem immediately obvious to some, exploring the various methods for solving this and similar problems provides a valuable foundation for tackling more complex percentage calculations. This article will delve into several approaches, explaining each step clearly and providing practical examples. We'll also discuss the real-world applications of percentage calculations.
Understanding Percentages
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." So, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this fundamental concept is crucial for solving any percentage problem.
Method 1: Using the Percentage Formula
The most straightforward way to solve "2 is what percent of 8?" is by using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 2 (the number we're comparing)
- Whole: 8 (the total number)
Plugging these values into the formula:
(2 / 8) * 100% = 0.25 * 100% = 25%
Therefore, 2 is 25% of 8.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation that states that two ratios are equal. We can set up a proportion to solve for the unknown percentage (x):
2/8 = x/100
To solve for x, we cross-multiply:
2 * 100 = 8 * x
200 = 8x
x = 200 / 8
x = 25
Therefore, x = 25%, confirming our previous result.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
First, express the relationship as a fraction: 2/8
Next, simplify the fraction: 2/8 = 1/4
Then, convert the fraction to a decimal by dividing the numerator by the denominator: 1 ÷ 4 = 0.25
Finally, multiply the decimal by 100% to express it as a percentage: 0.25 * 100% = 25%
This method highlights the direct link between fractions, decimals, and percentages.
Real-World Applications of Percentage Calculations
Percentage calculations are incredibly common in everyday life and across various professional fields. Here are just a few examples:
-
Calculating discounts: A store offers a 20% discount on an item priced at $50. The discount amount is 20% of $50, which is ($20), resulting in a final price of $30.
-
Determining tax rates: Understanding sales tax percentages is essential for budgeting and financial planning. If the sales tax is 6%, you'd calculate the tax amount on a purchase by multiplying the price by 0.06.
-
Analyzing financial statements: Businesses use percentages extensively to analyze financial data, such as profit margins, return on investment (ROI), and debt-to-equity ratios. These percentages provide valuable insights into a company's financial health and performance.
-
Understanding statistics: Percentages are fundamental in statistical analysis, allowing for easy comparison and interpretation of data. For instance, understanding the percentage of respondents who prefer a particular product helps businesses make informed decisions.
-
Calculating grades: Academic grades are often expressed as percentages, reflecting the proportion of correctly answered questions or the overall performance in a course.
-
Measuring growth rates: Percentage change is often used to track growth or decline in various aspects, such as population growth, economic growth, or stock market performance.
-
Cooking and baking: Many recipes use percentages to indicate the proportions of ingredients, particularly in baking, where precise measurements are vital.
-
Scientific experiments: In scientific research, percentages are used to express the concentration of solutions, the success rate of experiments, or the statistical significance of results.
Solving More Complex Percentage Problems
The fundamental principles discussed above can be applied to more complex percentage problems. For example:
Problem: If 15% of a number is 30, what is the number?
Solution:
Let's use the percentage formula again, but this time we'll solve for the "Whole":
(Part / Whole) * 100% = Percentage
We know:
- Part = 30
- Percentage = 15%
So the equation becomes:
(30 / Whole) * 100% = 15%
Solving for the Whole:
30 / Whole = 0.15
Whole = 30 / 0.15
Whole = 200
Therefore, the number is 200.
Problem: What percentage of 25 is 5?
Solution:
Using the formula:
(Part / Whole) * 100% = Percentage
- Part = 5
- Whole = 25
(5 / 25) * 100% = 0.2 * 100% = 20%
Therefore, 5 is 20% of 25.
Tips for Mastering Percentage Calculations
-
Practice regularly: The more you practice, the more comfortable you'll become with solving percentage problems.
-
Understand the underlying concepts: A solid grasp of fractions, decimals, and ratios is essential for understanding percentages.
-
Use different methods: Experiment with different approaches (formula, proportion, decimal conversion) to find the method that works best for you.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Utilize online resources and calculators: Many online resources and calculators can assist with more complex percentage problems. These tools can be valuable for verifying your answers and gaining a deeper understanding of the concepts.
-
Break down complex problems: If you encounter a challenging problem, break it down into smaller, more manageable steps.
-
Relate percentages to real-world situations: Connecting percentages to real-world examples can enhance your understanding and retention.
By mastering percentage calculations, you equip yourself with a valuable skill that extends far beyond the classroom. From managing your finances to analyzing data and understanding various aspects of everyday life, the ability to work confidently with percentages is an asset that will serve you well in many contexts. Remember to practice consistently and explore the different methods to build your expertise and confidence in solving percentage problems of all complexities.
Latest Posts
Latest Posts
-
Sic A Parrot On The Guild Emissary
Jul 06, 2025
-
How Many Slices Of Turkey Is 3 Oz
Jul 06, 2025
-
Which Word Best Describes The Tone Of The Passage
Jul 06, 2025
-
How Long Does It Take To Count To One Billion
Jul 06, 2025
-
Why Did The Kangaroo See A Psychiatrist
Jul 06, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.