2 Out Of 36 As A Percentage
Kalali
Apr 08, 2025 · 4 min read
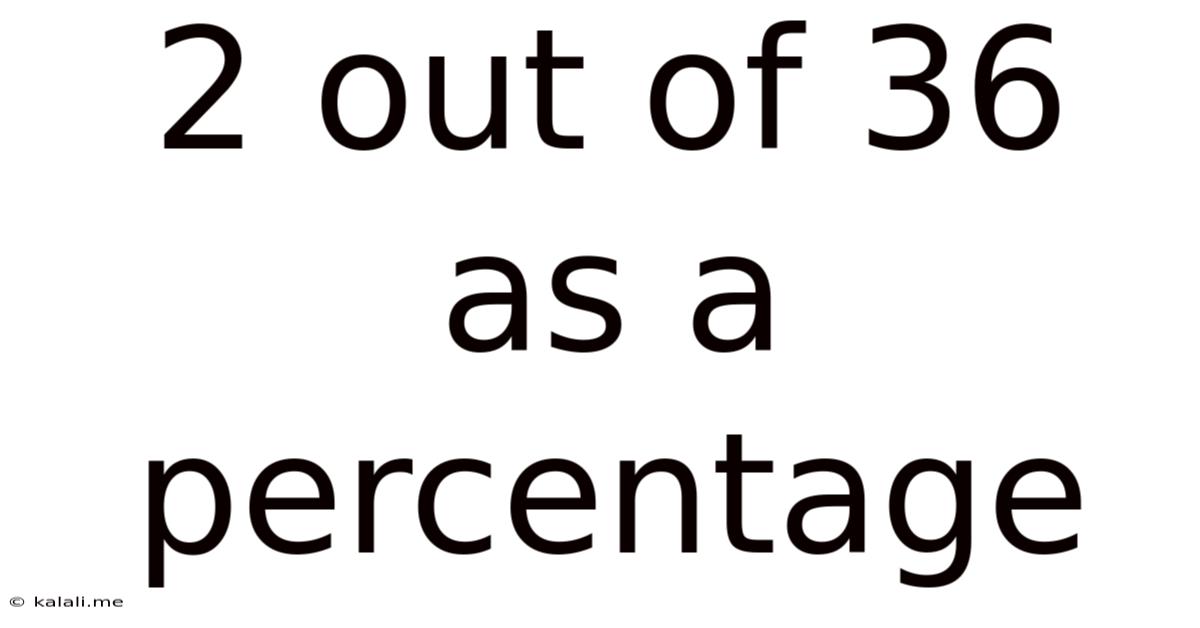
Table of Contents
2 out of 36 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions to percentages is especially crucial. This article will delve into the specific calculation of "2 out of 36 as a percentage," explaining the process in detail and expanding on broader percentage calculation techniques. We will also explore practical applications and address common misconceptions. This in-depth guide will equip you with the knowledge and confidence to tackle similar percentage problems with ease.
What is a Percentage?
Before jumping into the calculation, let's clarify what a percentage actually represents. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Percentages are a convenient way to express proportions and make comparisons, offering a standardized way to understand relative quantities.
Calculating 2 out of 36 as a Percentage: The Step-by-Step Approach
To determine what percentage 2 out of 36 represents, we follow these straightforward steps:
-
Express as a Fraction: First, write the given information as a fraction. In this case, it's 2/36.
-
Simplify the Fraction (Optional but Recommended): Simplifying the fraction makes subsequent calculations easier. Both the numerator (2) and the denominator (36) are divisible by 2. Simplifying gives us 1/18.
-
Convert to Decimal: To convert the fraction to a decimal, divide the numerator by the denominator: 1 ÷ 18 ≈ 0.0556 (we'll round for simplicity).
-
Convert to Percentage: Multiply the decimal by 100 to express it as a percentage: 0.0556 x 100 = 5.56%.
Therefore, 2 out of 36 is approximately 5.56%.
Understanding the Calculation: A Deeper Dive
The process of converting a fraction to a percentage involves fundamentally understanding the relationship between fractions, decimals, and percentages. They are all different ways of representing the same proportion.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number).
-
Decimals: Express numbers as powers of ten, providing a numerical representation of fractions.
-
Percentages: A specific type of decimal, scaled to represent parts of 100.
The conversion steps we followed effectively bridge these different representations. Simplifying the fraction before converting helps manage smaller numbers and reduces the risk of errors in division. Rounding the decimal is necessary for practical application, as the decimal can often continue infinitely.
Practical Applications: Where Percentage Calculations are Used
Understanding percentage calculations has wide-ranging practical applications:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations.
-
Statistics: Percentages are essential for presenting data in a clear and easily understandable format. This includes representing survey results, demographic breakdowns, and probability outcomes.
-
Science: Many scientific fields, such as chemistry and biology, frequently employ percentage calculations to express concentrations, yields, and error margins.
-
Education: Grading systems, test scores, and performance metrics are often expressed as percentages.
-
Everyday Life: Calculating tips, sales discounts, and understanding nutritional information all involve percentage calculations.
Common Misconceptions and Errors to Avoid
While percentage calculations are relatively straightforward, certain misconceptions can lead to errors:
-
Confusing Percentage Change with Absolute Change: Percentage change reflects the relative difference between two values, whereas absolute change represents the actual numerical difference. For example, a 10% increase from 100 is 10, but a 10% increase from 1000 is 100.
-
Incorrectly Applying Percentage Increases and Decreases: Successive percentage increases or decreases do not simply add or subtract. For instance, a 10% increase followed by a 10% decrease does not result in the original value.
-
Ignoring Significant Figures: Rounding too early or excessively can introduce inaccuracy into the final result.
-
Using Incorrect Formulas: Ensuring you use the appropriate formula for the specific percentage calculation is paramount.
Advanced Percentage Calculations: Beyond the Basics
While this article focuses on a basic percentage calculation, there are more advanced concepts to explore:
-
Percentage Increase and Decrease: Calculating the percentage change between two values.
-
Percentage Points: This refers to the actual numerical difference between two percentages, not a percentage change.
-
Compound Interest: Calculating interest earned on both the principal and accumulated interest.
-
Percentage of a Percentage: Finding a percentage of a percentage involves nested calculations.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a critical life skill with far-reaching implications. This detailed guide has explored the specific calculation of "2 out of 36 as a percentage," explaining the methodology step-by-step and highlighting common pitfalls. By grasping the underlying principles and practicing these techniques, you can confidently tackle various percentage problems in diverse contexts. Remember to always focus on accuracy, clarity, and a thorough understanding of the concepts involved. Mastering these calculations will significantly enhance your analytical capabilities and problem-solving skills. From simple everyday tasks to more complex scientific or financial calculations, the ability to confidently work with percentages is invaluable.
Latest Posts
Latest Posts
-
How Much Is 60 Cm In Feet
Apr 17, 2025
-
Cuanto Es 29 Grados Farenheit En Centigrados
Apr 17, 2025
-
What Is A 7 Out Of 9
Apr 17, 2025
-
How Do You Eliminate The Parameter
Apr 17, 2025
-
How Many Parallel Sides Does Trapezoid Have
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 2 Out Of 36 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.