2 Out Of 6 Is What Percent
Kalali
Apr 08, 2025 · 5 min read
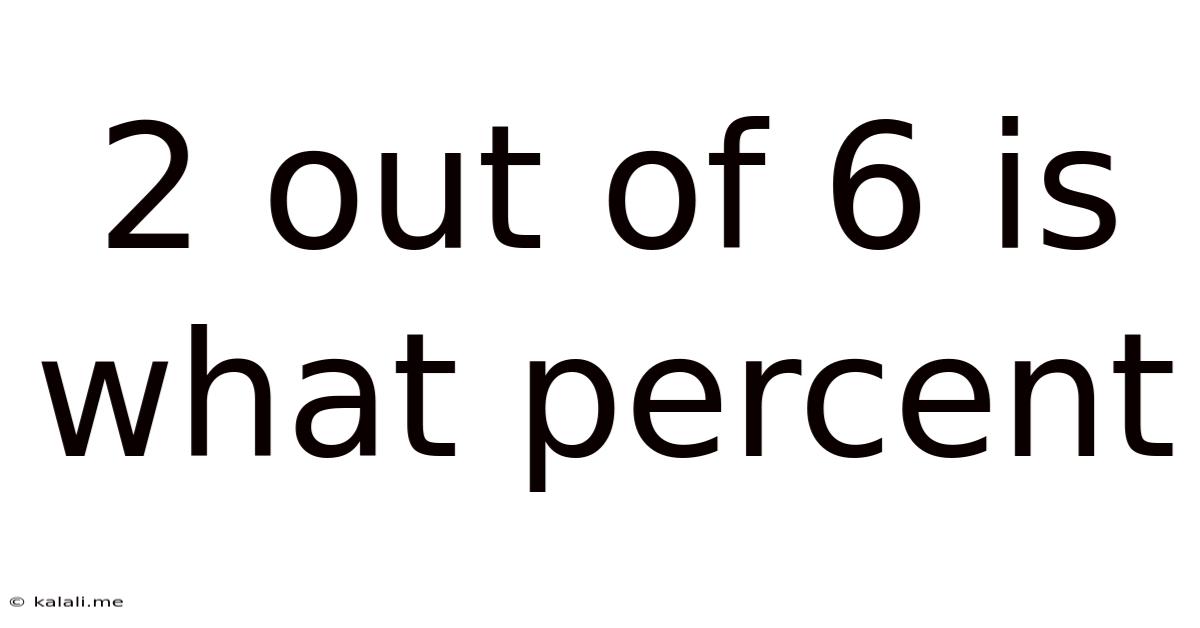
Table of Contents
2 Out of 6 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves into the calculation of percentages, specifically addressing the question: "2 out of 6 is what percent?" We'll explore different methods for solving this problem, discuss the underlying concepts, and provide practical examples to solidify your understanding. This guide will equip you with the knowledge to confidently tackle similar percentage calculations in the future.
Understanding Percentages: A Quick Recap
A percentage is a fraction or ratio expressed as a number out of 100. The symbol used to represent percentage is "%". Essentially, it represents a part of a whole, where the whole is always considered to be 100%. For instance, 50% means 50 out of 100, or half. Understanding this fundamental concept is crucial for accurately calculating percentages.
Method 1: Using the Fraction Method
The most straightforward method to determine the percentage is by converting the given ratio into a fraction and then converting that fraction into a percentage.
-
Step 1: Express the ratio as a fraction. The problem "2 out of 6" can be written as the fraction 2/6.
-
Step 2: Simplify the fraction (if possible). In this case, we can simplify 2/6 by dividing both the numerator (2) and the denominator (6) by their greatest common divisor, which is 2. This simplifies the fraction to 1/3.
-
Step 3: Convert the fraction to a decimal. To convert the fraction 1/3 to a decimal, divide the numerator (1) by the denominator (3). 1 ÷ 3 = 0.3333... (This is a repeating decimal).
-
Step 4: Convert the decimal to a percentage. Multiply the decimal by 100 to obtain the percentage. 0.3333... × 100 ≈ 33.33%.
Therefore, 2 out of 6 is approximately 33.33%. The three dots (...) indicate that the decimal is repeating infinitely. For practical purposes, rounding to two decimal places is usually sufficient.
Method 2: Using the Proportion Method
The proportion method offers another approach to solving percentage problems. This method involves setting up a proportion and solving for the unknown percentage.
-
Step 1: Set up a proportion. We can set up a proportion as follows:
x/100 = 2/6where 'x' represents the percentage we want to find.
-
Step 2: Cross-multiply. Cross-multiplying gives us:
6x = 200 -
Step 3: Solve for x. Divide both sides of the equation by 6:
x = 200/6x ≈ 33.33
Therefore, 2 out of 6 is approximately 33.33%. This method confirms the result obtained using the fraction method.
Method 3: Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage function. To calculate "2 out of 6 is what percent," you can perform the following steps:
- Divide 2 by 6: 2 ÷ 6 = 0.3333...
- Multiply the result by 100: 0.3333... × 100 ≈ 33.33%
This method provides a quick and efficient way to calculate percentages, particularly for more complex calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in many real-world scenarios. Here are a few examples:
-
Discounts: If a store offers a 20% discount on an item, you can calculate the discount amount and the final price by applying percentage calculations.
-
Taxes: Sales tax is typically expressed as a percentage, enabling you to calculate the total cost of an item, including tax.
-
Grade Calculation: In many educational systems, grades are often expressed as percentages, allowing for easy comparison of performance.
-
Financial Analysis: Percentage changes are commonly used in finance to track stock prices, investment returns, and other financial metrics.
-
Data Analysis: Percentages are essential for representing proportions and trends in data analysis, facilitating better understanding of data sets.
-
Surveys and Polls: Results from surveys and polls are often presented as percentages, making it easier to understand public opinion or preferences.
Expanding the Concept: Variations on the Theme
While we focused on "2 out of 6," the principles can be extended to other ratios. For example:
-
4 out of 10: This translates to 4/10 = 2/5 = 0.4 = 40%.
-
7 out of 20: This translates to 7/20 = 0.35 = 35%.
-
15 out of 50: This translates to 15/50 = 3/10 = 0.3 = 30%.
The fundamental steps—expressing the ratio as a fraction, simplifying if possible, converting to a decimal, and then to a percentage—remain the same regardless of the specific numbers involved.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, some common errors can arise:
-
Incorrect Fraction Formation: Ensure you correctly represent the ratio as a fraction; the "out of" part represents the denominator.
-
Improper Decimal to Percentage Conversion: Remember to multiply the decimal by 100 to obtain the percentage.
-
Rounding Errors: While rounding is sometimes necessary, be mindful of significant figures and avoid excessive rounding, especially in scientific or financial contexts.
-
Confusing Percentage Increase and Decrease: Remember that percentage increase and decrease calculations require different approaches.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a valuable skill applicable in numerous contexts. Understanding the various methods discussed—the fraction method, the proportion method, and the calculator method—allows you to approach percentage problems with confidence. Remember to carefully follow the steps, avoid common errors, and practice regularly to build proficiency. With consistent practice, percentage calculations will become second nature, empowering you to confidently tackle various quantitative challenges in your daily life, academic pursuits, and professional endeavors. Mastering percentages is not merely about numbers; it's about understanding the fundamental concept of representing parts of a whole, a skill that transcends mathematical calculations and finds applications in a wide range of disciplines.
Latest Posts
Latest Posts
-
How Much Is 84 In In Feet
Apr 17, 2025
-
What Is The Lowest Common Multiple Of 3 And 7
Apr 17, 2025
-
2 To The Power Of 40
Apr 17, 2025
-
Cuanto Son 73 Grados Fahrenheit En Centigrados
Apr 17, 2025
-
9 Meters Is How Many Feet
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 2 Out Of 6 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.