20 Is 40 Percent Of What Number
Kalali
Jul 13, 2025 · 5 min read
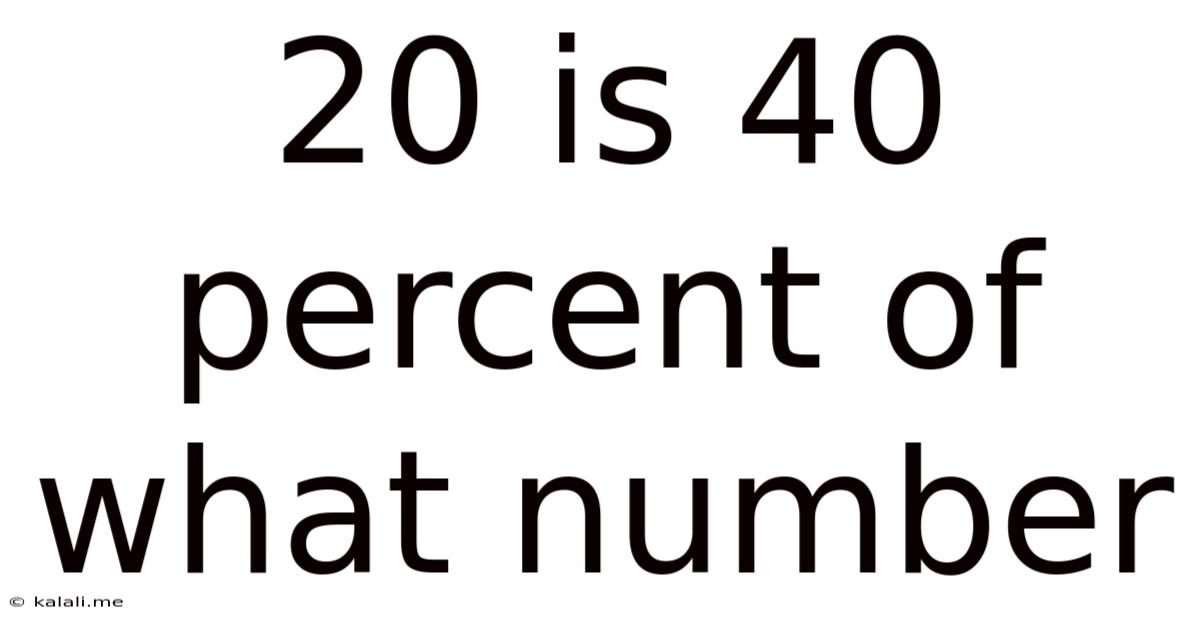
Table of Contents
20 is 40 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Finding a percentage of a number is a fundamental mathematical skill with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and analyzing statistical data. This article will delve into the question, "20 is 40 percent of what number?", providing a step-by-step solution, exploring various methods for solving percentage problems, and offering practical examples to solidify your understanding. This guide will also cover related concepts like finding the percentage increase or decrease, and working with different percentage representations (decimals and fractions).
Understanding Percentages:
A percentage is a fraction or ratio expressed as a number out of 100. It represents a proportion of a whole. The symbol "%" signifies "percent" or "out of 100." For instance, 40% means 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40.
Solving "20 is 40 Percent of What Number?"
The problem "20 is 40 percent of what number?" can be expressed as an equation:
20 = 0.40 * x
Where 'x' represents the unknown number we're trying to find. To solve for 'x', we need to isolate it on one side of the equation. We can do this by dividing both sides of the equation by 0.40:
x = 20 / 0.40
x = 50
Therefore, 20 is 40 percent of 50.
Alternative Methods for Solving Percentage Problems:
Several methods can be used to solve percentage problems, depending on your preference and the complexity of the problem. Here are a few common approaches:
1. Using Proportions:
Proportions are a powerful tool for solving percentage problems. We can set up a proportion based on the given information:
20/x = 40/100
This proportion states that the ratio of 20 to the unknown number (x) is equal to the ratio of 40 to 100. To solve this proportion, we can cross-multiply:
20 * 100 = 40 * x
2000 = 40x
x = 2000 / 40
x = 50
2. Using the Percentage Formula:
The basic percentage formula is:
(Part/Whole) * 100 = Percentage
In our problem, we know the "part" (20) and the "percentage" (40). We need to find the "whole" (x). We can rearrange the formula to solve for the whole:
Whole = (Part / Percentage) * 100
Whole = (20 / 40) * 100
Whole = 0.5 * 100
Whole = 50
3. Using Decimals:
We can directly convert the percentage to a decimal and solve the equation, as shown in the initial solution. This method is often the most straightforward and efficient.
Practical Applications of Percentage Calculations:
Percentage calculations are ubiquitous in various aspects of life:
-
Shopping: Calculating discounts, sales tax, and the final price of an item after applying discounts and taxes. For example, if a shirt costs $100 and is on sale for 20% off, the discount amount is $20 (20% of $100), and the final price is $80.
-
Finance: Understanding interest rates on loans and savings accounts, calculating investment returns, and analyzing financial statements. A 5% interest rate on a $1000 loan means an annual interest payment of $50.
-
Science and Statistics: Representing data in graphs and charts, calculating statistical measures like percentages and proportions, and analyzing experimental results.
-
Real Estate: Calculating property taxes, evaluating property value appreciation or depreciation, and understanding mortgage interest rates. An increase in property value by 10% represents a significant gain for the homeowner.
Advanced Percentage Concepts:
Beyond the basic calculations, understanding more advanced concepts can significantly enhance your ability to solve complex percentage problems:
1. Percentage Increase and Decrease:
Calculating percentage increase or decrease involves finding the difference between two values and expressing that difference as a percentage of the original value.
- Percentage Increase: [(New Value - Original Value) / Original Value] * 100
- Percentage Decrease: [(Original Value - New Value) / Original Value] * 100
For instance, if the price of a product increases from $50 to $60, the percentage increase is [(60-50)/50] * 100 = 20%.
2. Compound Interest:
Compound interest is interest calculated on the initial principal and also on the accumulated interest from previous periods. It leads to exponential growth of an investment or debt.
3. Percentage Points:
Percentage points represent the absolute difference between two percentages. For example, if the interest rate increases from 5% to 10%, it's a 5 percentage point increase, not a 100% increase.
4. Working with Fractions and Decimals:
It's crucial to be comfortable converting between percentages, fractions, and decimals. This flexibility is essential for solving various percentage problems effectively. Remember, 25% is equivalent to ¼ or 0.25.
Troubleshooting Common Percentage Mistakes:
Common mistakes in percentage calculations include:
-
Incorrectly converting percentages to decimals or fractions. Always double-check your conversions to ensure accuracy.
-
Mixing up the "part" and "whole" in the percentage formula. Understanding which value represents the part and which represents the whole is crucial.
-
Failing to account for compound interest when appropriate. When dealing with investments or loans over time, compound interest must be considered.
-
Confusing percentage points with percentage changes. Remember that percentage points refer to the absolute difference between percentages.
Conclusion:
Understanding percentages is a fundamental skill with far-reaching implications. This article has explored multiple methods for solving percentage problems, highlighting the solution to "20 is 40 percent of what number?" (50) and delving into various practical applications and advanced concepts. By mastering these techniques and avoiding common mistakes, you can confidently tackle a wide array of percentage-related challenges in various fields. Remember to practice regularly and apply your knowledge to real-world scenarios to solidify your understanding and improve your problem-solving skills.
Latest Posts
Latest Posts
-
When Was Christmas Last On A Wednesday
Jul 13, 2025
-
Welding Print Reading 8th Edition Answer Key
Jul 13, 2025
-
How Much Does A Case Of Soda Weigh
Jul 13, 2025
-
What Did The Boy Snake Say To The Girl Snake
Jul 13, 2025
-
Un Oso Y Un Amor In English
Jul 13, 2025
Related Post
Thank you for visiting our website which covers about 20 Is 40 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.