20 Is What Percent Of 10
Kalali
Apr 16, 2025 · 5 min read
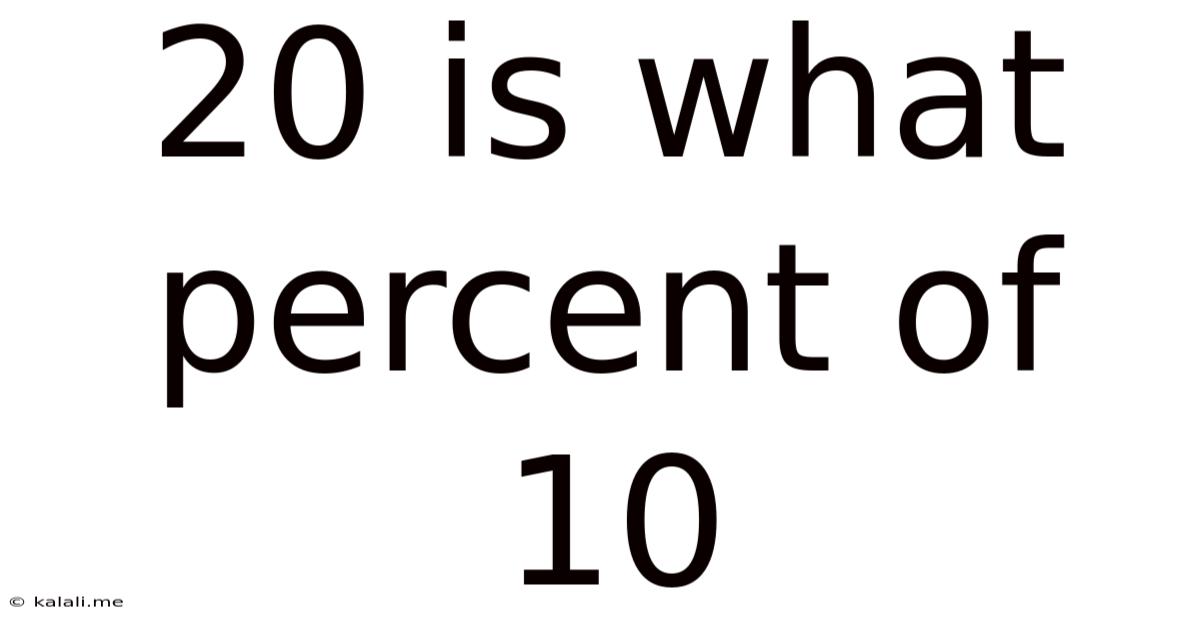
Table of Contents
20 is What Percent of 10? Understanding Percentages and Their Applications
This seemingly simple question, "20 is what percent of 10?", opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with wide-ranging applications in everyday life, finance, and numerous other fields. This article will not only answer the question directly but also delve into the underlying principles, providing various methods for solving percentage problems and showcasing practical examples. We'll explore the concept of percentages, discuss different approaches to calculating percentages, and look at real-world scenarios where this type of calculation is crucial.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental definition is key to solving percentage problems.
Solving "20 is What Percent of 10?"
The question "20 is what percent of 10?" might seem counterintuitive at first glance. It implies that a part (20) is larger than the whole (10), which isn't typically how we visualize percentages. However, this is perfectly possible and represents a percentage greater than 100%. Let's explore how to solve this using different methods.
Method 1: The Proportion Method
This method involves setting up a proportion, which equates two ratios. We can represent the problem as:
- Part/Whole = Percentage/100
In this case:
- Part = 20
- Whole = 10
- Percentage = x (what we need to find)
Substituting these values into the proportion, we get:
- 20/10 = x/100
To solve for x, we cross-multiply:
- 20 * 100 = 10 * x
- 2000 = 10x
- x = 2000/10
- x = 200
Therefore, 20 is 200% of 10.
Method 2: The Decimal Method
This method involves converting the problem into a decimal equation. First, we find the ratio of the part to the whole:
- 20/10 = 2
This ratio represents the decimal equivalent of the percentage. To convert this decimal to a percentage, we multiply by 100:
- 2 * 100 = 200%
This confirms our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function. To solve this using a calculator, you would typically enter:
- (20 / 10) * 100 = 200
This directly gives the answer in percentage form.
Understanding Percentages Greater Than 100%
The result of 200% might seem unusual, but percentages greater than 100% simply indicate that the "part" is more than the "whole." This is common in various contexts. For instance:
- Growth and Increase: If a company's profits increase from $10 million to $20 million, its profit increase is 200% of its initial profit.
- Comparative Analysis: If a product's sales increase from 10 units to 20 units, the sales have increased by 200%.
- Data Overruns: In project management, if the project's budget was initially $10,000 and the actual cost is $20,000, the cost overrun is 200% of the initial budget.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous everyday situations:
- Finance: Calculating interest rates, loan payments, discounts, taxes, profit margins, and investment returns all involve percentage calculations. For example, calculating the simple interest on a loan, determining the final price after a discount, or understanding the annual percentage yield (APY) on a savings account all rely on percentage calculations.
- Sales and Marketing: Analyzing sales growth, conversion rates, market share, customer acquisition costs, and return on investment (ROI) often requires calculating percentages.
- Science and Engineering: Percentages are used in expressing concentrations, efficiencies, and error margins in various scientific and engineering applications. For example, determining the percentage composition of a chemical compound or expressing the efficiency of a machine.
- Healthcare: Calculating medication dosages, interpreting laboratory results, and assessing treatment success often involve percentage calculations.
- Everyday Life: Calculating tips in restaurants, determining sale prices, understanding discounts and interest rates, all involve percentages.
Beyond the Basics: More Complex Percentage Problems
While the problem "20 is what percent of 10?" is relatively straightforward, more complex percentage problems exist:
- Finding the Whole: If 20% of a number is 10, what is the number? This requires working backwards and involves dividing 10 by 0.20 to get the whole (50).
- Finding the Part: What is 20% of 100? This involves multiplying 100 by 0.20 to get the part (20).
- Percentage Change: Calculating the percentage increase or decrease between two values. This involves finding the difference between the two values, dividing by the original value, and then multiplying by 100.
- Compound Interest: Calculating interest that accrues on both the principal and accumulated interest. This involves using exponential functions.
Mastering Percentage Calculations: Tips and Tricks
To improve your ability to solve percentage problems quickly and efficiently:
- Practice Regularly: The more you practice, the more comfortable you'll become with different approaches and problem types.
- Understand the Concepts: Ensure you have a strong understanding of the fundamental concepts of percentages, ratios, and proportions.
- Use Different Methods: Familiarize yourself with multiple methods (proportion, decimal, calculator) so you can choose the most suitable approach for each problem.
- Visual Aids: Visual aids like diagrams and charts can be helpful in understanding percentage relationships.
- Check Your Answers: Always check your answers to ensure accuracy. This is particularly important in financial calculations.
Conclusion: The Power of Percentages
Understanding how to solve percentage problems, even seemingly simple ones like "20 is what percent of 10?", is a valuable skill with wide-reaching applications. By mastering the fundamental concepts and practicing different calculation methods, you equip yourself with a crucial tool for navigating various aspects of life, from personal finance to professional endeavors. The ability to quickly and accurately interpret and manipulate percentages will undoubtedly prove invaluable in your academic pursuits and future career. Remember that while the answer to the initial question is 200%, the true value lies in grasping the underlying principles and their broader implications.
Latest Posts
Latest Posts
-
How Many Species Of Reptiles Are There
Apr 19, 2025
-
6 Cups Equals How Many Pints
Apr 19, 2025
-
How To Do Mole To Mass Conversions
Apr 19, 2025
-
Life Cycle Of A Plant Bean
Apr 19, 2025
-
How Do You Find The Mean In A Dot Plot
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.